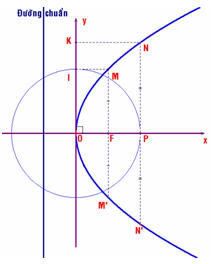
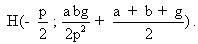 Cách 1. Xét cách vẽ parabol sau: “Trong mặt phẳng Oxy, cho parabol (P) có phương trình: Cách 1. Xét cách vẽ parabol sau: “Trong mặt phẳng Oxy, cho parabol (P) có phương trình: 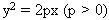 . Gọi M, N là các điểm nằm trên (P) có hoành độ lần lượt là p/2; p và có tung độ dương. Gọi I, K lần lượt là hình chiếu của M, N trên trục Oy. Tính tỉ số . Gọi M, N là các điểm nằm trên (P) có hoành độ lần lượt là p/2; p và có tung độ dương. Gọi I, K lần lượt là hình chiếu của M, N trên trục Oy. Tính tỉ số 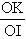 .” .”
Giải
Vì 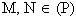 , nên thay các hoành độ p/2 và p vào phương trình của (P) ta được: , nên thay các hoành độ p/2 và p vào phương trình của (P) ta được:
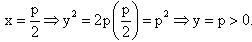
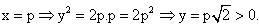
Vì I, K lần lượt là hình chiếu của M, N trên trục Oy nên:
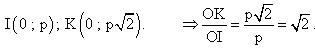
Cách dựng parabol (P).
Từ bài toán trên, ta suy ra cách dựng (P): 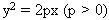 trong mặt phẳng Oxy dựa vào 5 điểm như sau: trong mặt phẳng Oxy dựa vào 5 điểm như sau:
Hiện hệ trục Oxy.
Dựng tiêu điểm F(p/2 ; 0).
Phép đối xứng tâm F biến gốc toạ độ O thành điểm P.
Dựng đường tròn tâm O, bán kính OP cắt phần dương của trục Oy tại I.
Phép vị tự tâm O tỉ số 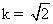 biến điểm I thành điểm K. biến điểm I thành điểm K.
Đường vuông góc với Ox tại F và đường vuông góc với Oy tại I cắt nhau tại M.
Đường vuông góc với Ox tại P và đường vuông góc với Oy tại K cắt nhau tại N.
Phép đối xứng trục Ox biến điểm M thành 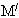 và biến điểm N thành và biến điểm N thành 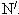 . .
Cônic qua 5 điểm 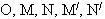 là parabol cần dựng. là parabol cần dựng.
Muốn biết phương trình của (P) ta thực hiện : 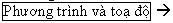 kích vào (P), khi đó ta có ngay phương trình của (P). kích vào (P), khi đó ta có ngay phương trình của (P).
Cách 2. Ta có thể vẽ prarabol theo một cách khác, đó là dựa vào định nghĩa của parabol. Cách trình bày này hơi dài. Nhưng cũng xin được đưa ra cho các bạn theo dõi. Từ cơ sở toán, bạn đọc hãy tự đưa ra cách dựng tương ứng cho chúng.
Định nghĩa 1
Parabol là quỹ tích của tâm các đường tròn tiếp xúc với một đường thẳng d và đi qua một điểm F không nằm trên d. d gọi là đường chuẩn. F gọi là tiêu điểm.
Định nghĩa 2
Xét một đường tròn (C), tâm M và đi qua F. Hạ ME vuông góc với d. Điều kiện cần và đủ để cho (C) tiếp xúc với d là: MF = ME.
Từ đây ta có định nghĩa:
Quỹ tích những điểm cách đều một điểm cố định F và một đường thẳng cố định d (không qua F) là parabol mà tiêu điểm là F, đường chuẩn d.
Ta có bài toán sau:
Bài toán 1. Cho một đường tròn (O) và một đường thẳng d tiếp xúc nhau tại A. Tìm quỹ tích tâm M của đường tròn tiếp xúc với (O) và d.
Ta chứng minh như sau:
Nếu một đường tròn tiếp xúc với d ở A thì nó tiếp xúc luôn với (O) ở A. Quỹ tích của M ở trong trường hợp này là đường thẳng vuông góc với d ở A.
Giả sử (M) tiếp xúc với (O) ở T và tiếp xúc với d ở H. T và H khác nhau. Kéo dài MH một đoạn HE = OA. Khi H vạch nên d thì E vạch nên d1, suy từ d ra bằng phép tịnh tiến mà vector có hướng là vector OA. Ta luôn luôn có: MO = MT + TO; ME = MH + HE hay MO = ME.
Vậy quỹ tích của M là parabol mà tiêu điểm là O, đường chuẩn là d1.
 Từ đây ta có một số cách vẽ parabol: Từ đây ta có một số cách vẽ parabol:
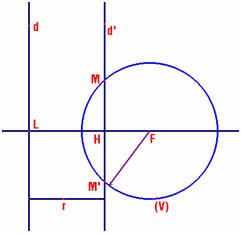
a) Cho tiêu điểm F, đường chuẩn d và điểm E. Muốn tìm một điểm M tương ứng thì kẻ Et vuông góc với d. Vẽ trung trực của EF. Chúng cắt nhau tại M. Ta có MF = ME cho nên M là một điểm của parabol.
b) Cho ME = MF = r. Muốn tìm điểm M thì vẽ:
. Đường tròn (V) tâm F, bán kính r.
. Đường thẳng d’, cách d một khoảng là r (về phía F).
Nếu đường tròn và đường thẳng cắt nhau ở hai điểm M, M’ thì đó là hai điểm ở trên parabol. Để cho d’ cắt (V), điều kiện cần và đủ để FH < r là: |FL – LH| < r; hay 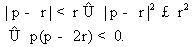 Hay giải ra, ta có : Hay giải ra, ta có : 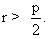
Bạn đọc có thể tham khảo một cách chi tiết các các vẽ trong các sách “Vẽ kỹ thuật”. Sau đây là một số bài tập về parabol. Tôi đưa ra lời giải bằng phương pháp toán học và các bạn đưa ra cách dựng và tìm quỹ tích cho chúng.
Bài toán 2. Trong hệ trục vuông góc Oxy, cho đường tròn (C) tâm I(a; O) qua gốc toạ độ O. Một đường tròn ( w ) di động tiếp xúc với Oy và trực giao với (C). Tìm hệ thức giữa toạ độ x, y của tâm . Suy ra quỹ tích của w .
Giải
Gọi (x; y) là toạ độ tâm w, bán kính đường tròn ( w ) cũng là x.
Ta có: 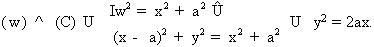 Vậy, quỹ tích tâm w là parabol Vậy, quỹ tích tâm w là parabol 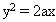
Bài toán 3. Cho 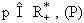 là parabol có phương trình là parabol có phương trình 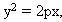 , F là tiêu điểm của nó. Một đường thẳng di động d đi qua F cắt P tại hai điểm kí hiệu là A, B. Xác định quỹ tích của tâm w của đường tròn ngoại tiếp tam giác OAB. , F là tiêu điểm của nó. Một đường thẳng di động d đi qua F cắt P tại hai điểm kí hiệu là A, B. Xác định quỹ tích của tâm w của đường tròn ngoại tiếp tam giác OAB.
Giải
Giả sử 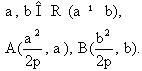 Ta có các phương trình của các đường trung trực của OA và OB là : Ta có các phương trình của các đường trung trực của OA và OB là : 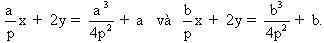 Từ đó ta suy ra các toạ độ (X, Y) của w: Từ đó ta suy ra các toạ độ (X, Y) của w: 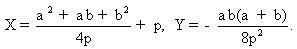 Mặt khác: Mặt khác: 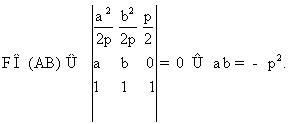 Từ đó kí hiệu S = a + b : Từ đó kí hiệu S = a + b : 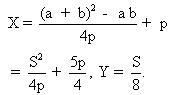
Cho S biến thiên khắp i , ta sẽ có phương trình của quỹ tích của w :
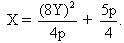 Hay quỹ tích là parabol có phương trình: Hay quỹ tích là parabol có phương trình: 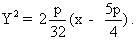
Bài toán 4. Cho parabol 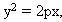 . M là một điểm của Parabol. Pháp tuyến tại M cắt Ox tại N. I là trung điểm của MN. Đường thẳng song song với Oy qua I cắt parabol tại P và Ox tại Q. Chứng minh MN = PQ và tìm quỹ tích của I khi M chuyển động trên Parabol. . M là một điểm của Parabol. Pháp tuyến tại M cắt Ox tại N. I là trung điểm của MN. Đường thẳng song song với Oy qua I cắt parabol tại P và Ox tại Q. Chứng minh MN = PQ và tìm quỹ tích của I khi M chuyển động trên Parabol.
Giải
Gọi 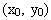 là toạ độ của M. Phương trình của pháp tuyến qua M là: là toạ độ của M. Phương trình của pháp tuyến qua M là: 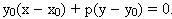 . Pháp tuyến này cắt Ox tại N. Hoành độ của trung điểm I của MN là: . Pháp tuyến này cắt Ox tại N. Hoành độ của trung điểm I của MN là: 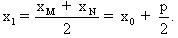
Phương trình của đường thẳng qua I song song với Oy là: 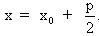 Tung độ của P được suy ra từ Tung độ của P được suy ra từ 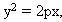 và từ đó và từ đó 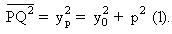
Ta có : 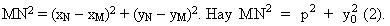
(1) và (2) cho ta MN = PQ.
Điểm M có toạ độ là 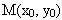 điểm N có toạ độ là điểm N có toạ độ là 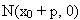 . Do đó, trung điểm I của MN có toạ độ là . Do đó, trung điểm I của MN có toạ độ là 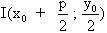 . Từ . Từ 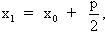 , ta được , ta được 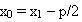 và từ và từ 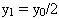 ta được ta được 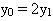 . .
Do 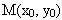 là một điểm của parabol nên là một điểm của parabol nên 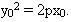 . Từ đó, ta có: . Từ đó, ta có: 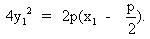 Vậy quỹ tích của I là parabol có phương trình là Vậy quỹ tích của I là parabol có phương trình là 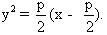
Bài toán 5. Cho parabol 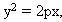 ; M, N, P là ba điểm trên parabol có tung độ là Các tiếp tuyến của parabol tại M, N, P đôi một cắt nhau tại C, A, B. Tìm quỹ tích của trực tâm tam giác ABC khi M, N, P chuyển động. ; M, N, P là ba điểm trên parabol có tung độ là Các tiếp tuyến của parabol tại M, N, P đôi một cắt nhau tại C, A, B. Tìm quỹ tích của trực tâm tam giác ABC khi M, N, P chuyển động.
Giải
Các điểm M, N, P có toạ độ là 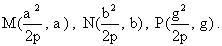 Các tiếp tuyến D1, D2, D3 của parabol tại M, N, P có phương trình là : Các tiếp tuyến D1, D2, D3 của parabol tại M, N, P có phương trình là :
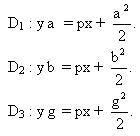
Giao điểm C của D1, D2 có toạ độ là 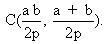 Giao điểm A của D2, D3 và giao điểm B của D3, D1 theo thứ tự có toạ độ là Giao điểm A của D2, D3 và giao điểm B của D3, D1 theo thứ tự có toạ độ là 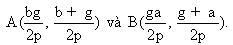
Vector BC có toạ độ là 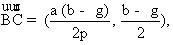 hay là hay là 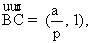 phương trình của đường cao AK của tam giác ABC là: phương trình của đường cao AK của tam giác ABC là: 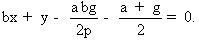
Giao điểm H của đường cao AK với đường chuẩn 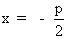 có toạ độ là : có toạ độ là : 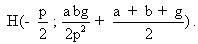
Vì tung độ của điểm H là một biểu thức đối xứng của suy ra các đường cao còn lại của tam giác ABC cùng cắt đường chuẩn tại H.
Do đó, H là trực tâm của tam giác ABC và quỹ tích của H là đường chuẩn của parabol đã cho.
Bài viết này đã kết thúc cơ sở toán của các thiết diện cônic.
( Nguyễn Ngọc Giang - 229/85 - Thích Quảng Đức -
Phường 4 - Quận Phú Nhuận - TP. Hồ Chí Minh )
School@net (Theo THNT)
|

 Xem giỏ hàng
Xem giỏ hàng Tôi đã giới thiệu với các bạn những điều quan trọng của phép dựng elip, hyperbol. Tôi xin giới thiệu tiếp với các bạn cơ sở toán của phép dựng parabol. Đây là điều tối quan trọng khi làm việc với parabol. Ta sẽ tìm hiểu cơ sở toán của phép dựng parabol khi đi đến với cách giải sau:
Tôi đã giới thiệu với các bạn những điều quan trọng của phép dựng elip, hyperbol. Tôi xin giới thiệu tiếp với các bạn cơ sở toán của phép dựng parabol. Đây là điều tối quan trọng khi làm việc với parabol. Ta sẽ tìm hiểu cơ sở toán của phép dựng parabol khi đi đến với cách giải sau: Cách 1. Xét cách vẽ parabol sau: “Trong mặt phẳng Oxy, cho parabol (P) có phương trình:
Cách 1. Xét cách vẽ parabol sau: “Trong mặt phẳng Oxy, cho parabol (P) có phương trình: 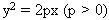 . Gọi M, N là các điểm nằm trên (P) có hoành độ lần lượt là p/2; p và có tung độ dương. Gọi I, K lần lượt là hình chiếu của M, N trên trục Oy. Tính tỉ số
. Gọi M, N là các điểm nằm trên (P) có hoành độ lần lượt là p/2; p và có tung độ dương. Gọi I, K lần lượt là hình chiếu của M, N trên trục Oy. Tính tỉ số 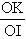 .”
.”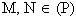 , nên thay các hoành độ p/2 và p vào phương trình của (P) ta được:
, nên thay các hoành độ p/2 và p vào phương trình của (P) ta được: 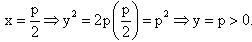
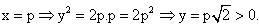
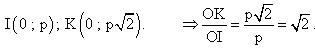
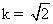 biến điểm I thành điểm K.
biến điểm I thành điểm K.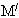 và biến điểm N thành
và biến điểm N thành 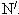 .
.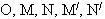 là parabol cần dựng.
là parabol cần dựng. kích vào (P), khi đó ta có ngay phương trình của (P).
kích vào (P), khi đó ta có ngay phương trình của (P).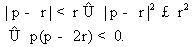 Hay giải ra, ta có :
Hay giải ra, ta có : 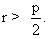
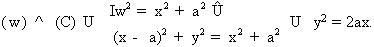 Vậy, quỹ tích tâm w là parabol
Vậy, quỹ tích tâm w là parabol 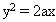
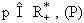 là parabol có phương trình
là parabol có phương trình 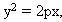 , F là tiêu điểm của nó. Một đường thẳng di động d đi qua F cắt P tại hai điểm kí hiệu là A, B. Xác định quỹ tích của tâm w của đường tròn ngoại tiếp tam giác OAB.
, F là tiêu điểm của nó. Một đường thẳng di động d đi qua F cắt P tại hai điểm kí hiệu là A, B. Xác định quỹ tích của tâm w của đường tròn ngoại tiếp tam giác OAB.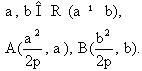 Ta có các phương trình của các đường trung trực của OA và OB là :
Ta có các phương trình của các đường trung trực của OA và OB là : 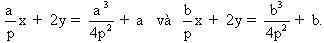 Từ đó ta suy ra các toạ độ (X, Y) của w:
Từ đó ta suy ra các toạ độ (X, Y) của w: 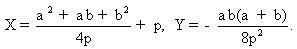 Mặt khác:
Mặt khác: 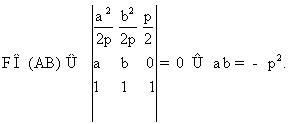 Từ đó kí hiệu S = a + b :
Từ đó kí hiệu S = a + b : 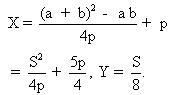
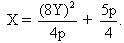 Hay quỹ tích là parabol có phương trình:
Hay quỹ tích là parabol có phương trình: 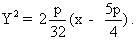
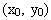 là toạ độ của M. Phương trình của pháp tuyến qua M là:
là toạ độ của M. Phương trình của pháp tuyến qua M là: 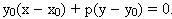 . Pháp tuyến này cắt Ox tại N. Hoành độ của trung điểm I của MN là:
. Pháp tuyến này cắt Ox tại N. Hoành độ của trung điểm I của MN là: 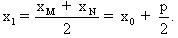
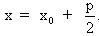 Tung độ của P được suy ra từ
Tung độ của P được suy ra từ 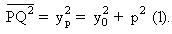
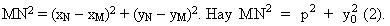
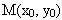 điểm N có toạ độ là
điểm N có toạ độ là 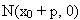 . Do đó, trung điểm I của MN có toạ độ là
. Do đó, trung điểm I của MN có toạ độ là 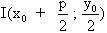 . Từ
. Từ 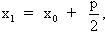 , ta được
, ta được 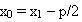 và từ
và từ 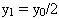 ta được
ta được 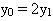 .
.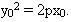 . Từ đó, ta có:
. Từ đó, ta có: 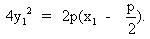 Vậy quỹ tích của I là parabol có phương trình là
Vậy quỹ tích của I là parabol có phương trình là 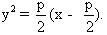
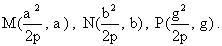 Các tiếp tuyến D1, D2, D3 của parabol tại M, N, P có phương trình là :
Các tiếp tuyến D1, D2, D3 của parabol tại M, N, P có phương trình là : 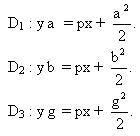
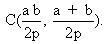 Giao điểm A của D2, D3 và giao điểm B của D3, D1 theo thứ tự có toạ độ là
Giao điểm A của D2, D3 và giao điểm B của D3, D1 theo thứ tự có toạ độ là 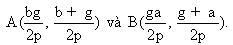
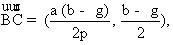 hay là
hay là 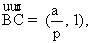 phương trình của đường cao AK của tam giác ABC là:
phương trình của đường cao AK của tam giác ABC là: 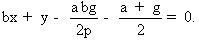
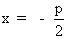 có toạ độ là :
có toạ độ là :