1. Định nghĩa
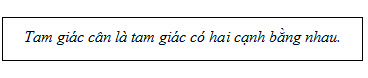
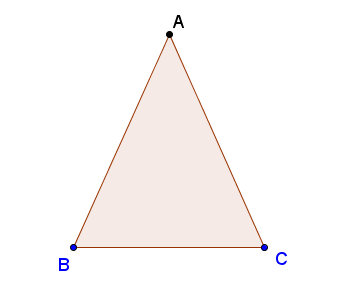
Trên hình 111, ta có tam giác cân ABC (AB = AC). Ta gọi AB và AC là các cạnh bên, BC là cạnh đáy, 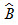 và và 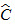 là các góc ở đáy, là các góc ở đáy, 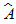 là góc ở đỉnh. là góc ở đỉnh.
Tam giác ABC có AB = AC còn được gọi là tam giác ABC cân tại A.
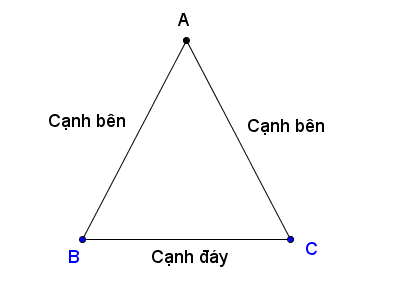
Hình 111
Tải trực tiếp tệp hình học động: L7_ch2_h111.ggb Xem trực tiếp hình vẽ động trên màn hình.
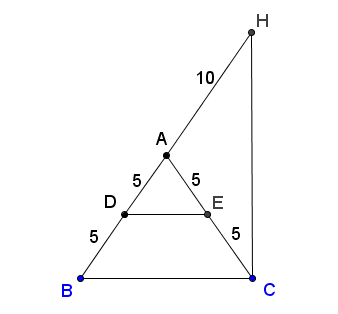
Hình 112
Tải trực tiếp tệp hình học động: L7_ch2_h112.ggb Xem trực tiếp hình vẽ động trên màn hình.
?1Tìm các tam giác cân trên hình 112. Kể tên các cạnh bên, cạnh đáy, góc ở đáy, góc ở đỉnh của các tam giác cân đó.
2. Tính chất
Cho tam giác ABC cân tại A. Tia phân giác của góc A cắt BC ở D (h.113). Hãy so sánh và .
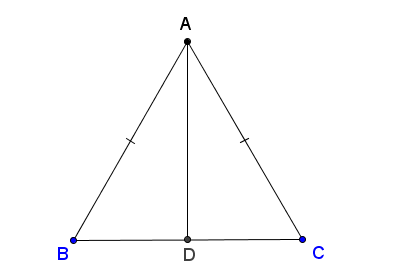
Hình 113
Tải trực tiếp tệp hình học động: L7_ch2_h113.ggb Xem trực tiếp hình vẽ động trên màn hình.
Ta có định lí 1 :

- Ngược lại, ta cũng chứng minh được định lí 2 (xem bài tập 44) :

Định nghĩa : Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau (h.114).
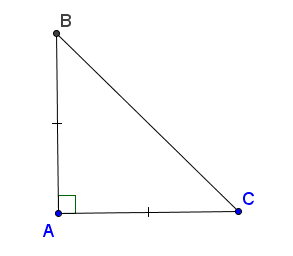
Hình 114
Tải trực tiếp tệp hình học động: L7_ch2_h114.ggb Xem trực tiếp hình vẽ động trên màn hình.
?3Tính số đo mỗi góc nhọn của một tam giác vuông cân.
3. Tam giác đều
Định nghĩa : Tam giác đều là tam giác có ba cạnh bằng nhau.
?4Vẽ tam giác đều ABC (h.115)
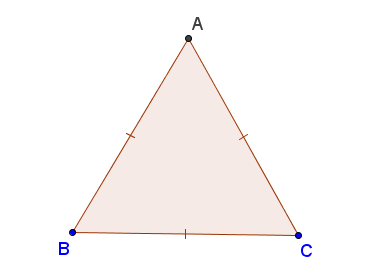
Hình 115
Tải trực tiếp tệp hình học động: L7_ch2_h115.ggb Xem trực tiếp hình vẽ động trên màn hình.
a) Vì sao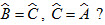 ? ?
b) Tính số đo mỗi góc của tam giác ABC.
- Từ các định lí 1 và 2, ta có các hệ quả :
- Trong một tam giác đều, mỗi góc bằng 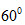 . .
- Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
- Nếu một tam giác cân có một góc bằng 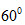 thì tam giác đó là tam giác đều. thì tam giác đó là tam giác đều.
BÀI TẬP
46. a) Dùng thước có chia xentimét và compa vẽ tam giác ABC cân tại B có cạnh đáy bằng 3cm, cạnh bên bằng 4cm.
b) Dùng thước có chia xentimét và compa vẽ tam giác đều ABC có cạnh bằng 3cm.
47. Trong các tam giác trên các hình 116, 117, 118 tam giác nào là tam giác cân, tam giác nào là tam giác đều ? Vì sao ?
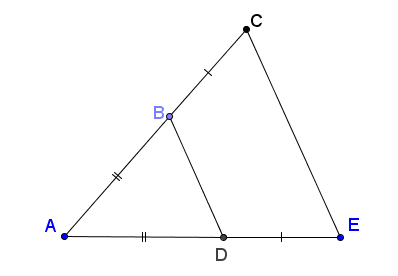
Hình 116
Tải trực tiếp tệp hình học động: L7_ch2_h116.ggb Xem trực tiếp hình vẽ động trên màn hình.
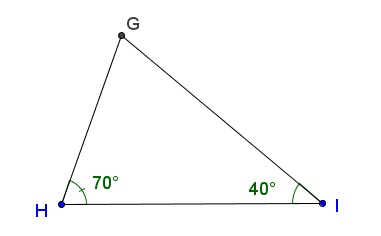
Hình 117
Tải trực tiếp tệp hình học động: L7_ch2_h117.ggb Xem trực tiếp hình vẽ động trên màn hình.
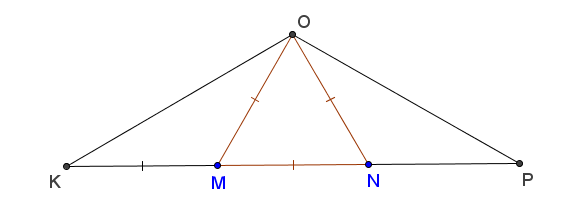
Hình 118
Tải trực tiếp tệp hình học động: L7_ch2_h118.ggb Xem trực tiếp hình vẽ động trên màn hình.
48. Cắt một tấm bìa hình tam giác cân. Hãy gấp tấm bìa đó sao cho hai cạnh bên trùng nhau để kiểm tra rằng hai góc ở đáy bằng nhau.
49. a) Tính các góc ở đáy của một tam giác cân biết góc ở đỉnh bằng  . .
b) Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng  . .
LUYỆN TẬP
50. Hai thanh AB và AC của vì kèo một mái nhà thường bằng nhau (h.119) và thường tạo với nhau một góc bằng :
a)  nếu mái là tôn. nếu mái là tôn.
b) 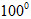 nếu mái là ngói. nếu mái là ngói.
Tính góc ABC trong từng trường hợp.
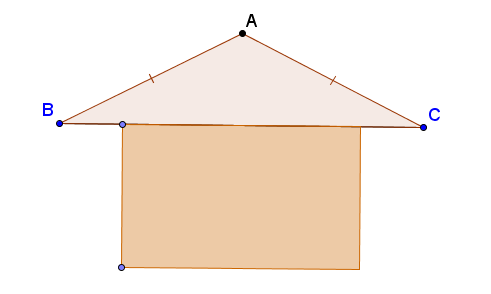
Hình 119
Tải trực tiếp tệp hình học động: L7_ch2_h119.ggb Xem trực tiếp hình vẽ động trên màn hình.
51. Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE.
a) So sánh 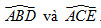 . .
b) Gọi I là giao điểm của BD và CE. Tam giác IBC là tam giác gì ? Vì sao ?
52. Cho góc xOy có số đo 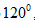 , điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B , điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B Ox), kẻ AC vuông góc với Oy (C Ox), kẻ AC vuông góc với Oy (C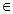 Oy). Tam giác ABC là tam giác gì ? Vì sao ? Oy). Tam giác ABC là tam giác gì ? Vì sao ?
Bài đọc thêm
Giả thiết và kết luận của định lí 1 và định lí 2 ở trang 126 có thể viết như sau (h.120) :
Hình 120
Tải trực tiếp tệp hình học động: L7_ch2_h120.ggb Xem trực tiếp hình vẽ động trên màn hình.
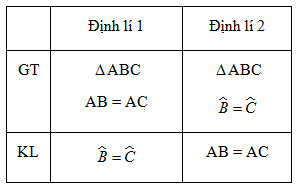
Ta thấy : 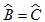 là giả thiết của định lí 2 nhưng là kết luận của định lí 1, AB = AC là kết luận của định lí 2 nhưng là giả thiết của định lí 1. Nếu gọi định lí 1 là định lí thuận thì định lí 2 là định lí đảo. là giả thiết của định lí 2 nhưng là kết luận của định lí 1, AB = AC là kết luận của định lí 2 nhưng là giả thiết của định lí 1. Nếu gọi định lí 1 là định lí thuận thì định lí 2 là định lí đảo.
Ta có thể viết gộp hai định lí 1 và 2 nói trên như sau :
Với mọi 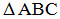 : :

Kí hiệu “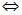 ” đọc là khi và chỉ khi. ” đọc là khi và chỉ khi.
Nếu có X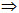 Y và có Y Y và có Y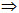 X thì ta có thể viết X X thì ta có thể viết X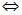 Y. Y.
Một số ví dụ về các định lí thuận và đảo :
Ví dụ 1. Xét hai đường thẳng bị cắt bởi đường thẳng thứ ba.
Định lí thuận : Nếu hai góc so le trong bằng nhau thì hai đường thẳng song song.
Định lí đảo : Nếu hai đường thẳng song song thì hai góc so le trong bằng nhau.
Ví dụ 2.
Định lí thuận : Trong một tam giác đều, ba góc bằng nhau.
Định lí đảo : Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
Chú ý rằng không phải định lí nào cũng có định lí đảo.
Chẳng hạn với định lí : Hai góc đối đỉnh thì bằng nhau, câu phát biểu đảo : Hai góc bằng nhau thì đối đỉnh không đúng, nó không phải là một định lí.
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng
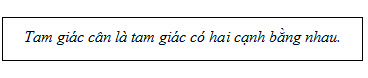
 và
và  là các góc ở đáy,
là các góc ở đáy, 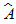 là góc ở đỉnh.
là góc ở đỉnh.






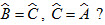 ?
?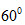 .
.


 .
. nếu mái là tôn.
nếu mái là tôn. 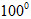 nếu mái là ngói.
nếu mái là ngói.
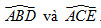 .
.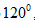 , điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B
, điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B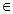 Ox), kẻ AC vuông góc với Oy (C
Ox), kẻ AC vuông góc với Oy (C

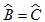 là giả thiết của định lí 2 nhưng là kết luận của định lí 1, AB = AC là kết luận của định lí 2 nhưng là giả thiết của định lí 1. Nếu gọi định lí 1 là định lí thuận thì định lí 2 là định lí đảo.
là giả thiết của định lí 2 nhưng là kết luận của định lí 1, AB = AC là kết luận của định lí 2 nhưng là giả thiết của định lí 1. Nếu gọi định lí 1 là định lí thuận thì định lí 2 là định lí đảo.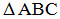 :
: 
 ” đọc là khi và chỉ khi.
” đọc là khi và chỉ khi. Y và có Y
Y và có Y

