1. Đường cao của tam giác
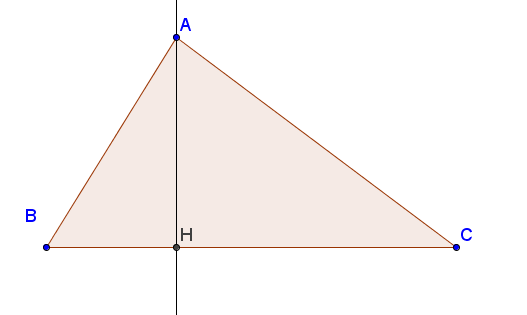
Hình 53
Tải trực tiếp tệp hình học động:L7_Ch3_h53.ggb Xem trực tiếp hình vẽ động trên màn hình.
Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.
Trong hình 53, đoạn thẳng AI là một đường cao của tam giác ABC. Ta còn nói AI là đường cao xuất phát từ đỉnh A (của tam giác ABC).
Đôi khi ta cũng gọi đường thẳng AI là một đường cao của tam giác ABC.
Mỗi tam giác có ba đường cao.
2. Tính chất ba đường cao của tam giác
?1 Dùng êke vẽ ba đường cao của tam giác ABC.
Hãy cho biết ba đường cao của tam giác đó có cùng đi qua một điểm hay không .
Ta thừa nhận điều dưới đây :
Định lí

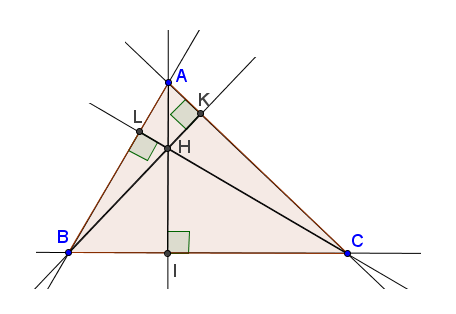
Hình 54
Tải trực tiếp tệp hình học động:L7_Ch3_h54.ggb Xem trực tiếp hình vẽ động trên màn hình.
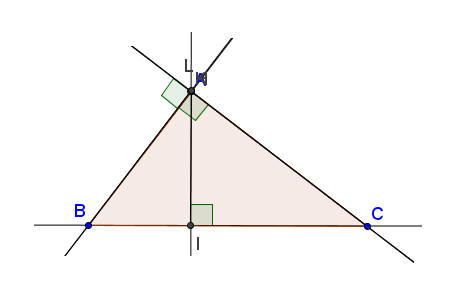
Hình 54b
Tải trực tiếp tệp hình học động:L7_Ch3_h54b.ggb Xem trực tiếp hình vẽ động trên màn hình.
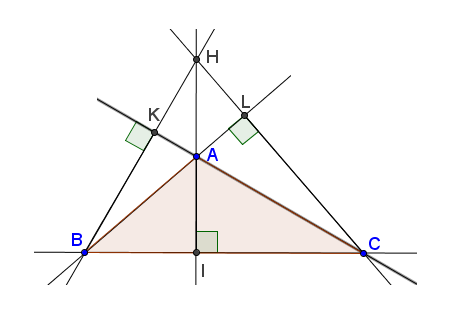
Hình 54c
Tải trực tiếp tệp hình học động:L7_Ch3_h54c.ggb Xem trực tiếp hình vẽ động trên màn hình.
Cụ thể (xem các hình 54a, b, c) : Ba đường cao AI, BK, CL cùng đi qua (đồng quy tại) điểm H.
Điểm H gọi là trực tâm của tam giác ABC.
3. Về các đường cao, trung tuyến, trung trực, phân giác của tam giác cân
Từ các điều đã biết trong bài 6 và bài 8, ta có tính chất sau :
Tính chất của tam giác cân
Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó (h.55).
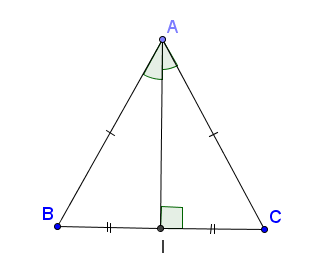
Hình 55
Tải trực tiếp tệp hình học động:L7_Ch3_h55.ggb Xem trực tiếp hình vẽ động trên màn hình.
Ngược lại với tính chất trên, ta có:
Nhận xét :
Trong một tam giác, nếu hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của đỉnh này) trùng nhau thì tam giác đó là một tam giác cân.
Thật vậy, bài tập 42 cho thấy : “Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân”; bài tập 52 cho thấy : “Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực (cùng ứng với một cạnh), thì tam giác đó là một tam giác cân”.
?2 Hãy phát biểu và chứng minh các trường hợp còn lại của nhận xét trên (xem như những bài tập).
Đặc biệt đối với tam giác đều, từ tính chất trên ta suy ra :
Trong tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau (h. 56).
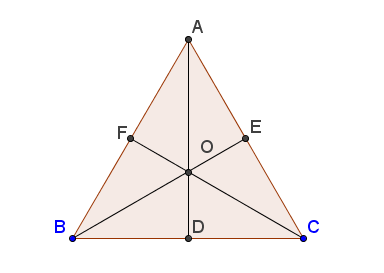
Hình 56
Tải trực tiếp tệp hình học động:L7_Ch3_h56.ggb Xem trực tiếp hình vẽ động trên màn hình.
Luyện tập
58. Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác.
59. Cho hình 57.
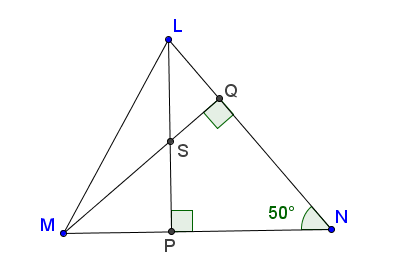
Hình 57
Tải trực tiếp tệp hình học động:L7_Ch3_h57.ggb Xem trực tiếp hình vẽ động trên màn hình.
a) Chứng minh NS ⊥ LM.
b) Khi 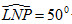 , hãy tính góc MSP và góc PSQ. , hãy tính góc MSP và góc PSQ.
60. Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K).
Kẻ đường thẳng vuông góc với d tại J. Trên lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt tại N.
Chứng minh rằng KN ⊥ IM.
61. Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.
62. Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng








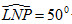 , hãy tính góc MSP và góc PSQ.
, hãy tính góc MSP và góc PSQ. 

