Trong tam giác ABC, nếu gọi O là điểm chung của ba đường trung trực (tâm đường tròn ngoại tiếp), G là điểm chung của ba đường trung tuyến (trọng tâm), H là điểm chung của ba đường cao (trực tâm), thì O, G, H cùng thuộc một đường thẳng ( G ở giữa O, H và OH = 3OG). Đường thẳng chứa O, G, H gọi là đường thẳng Ơ-le của tam giác ABC ; nó được mang tên nhà toán học lỗi lạc Lê-ô-na Ơ-le (1707 - 1783). Lê-ô-na Ơ-le sinh ra ở Thụy Sĩ, làm việc nhiều năm ở Nga. Số lượng công trình nghiên cứu khoa học của ông ít ai sánh kịp.
Bảng tổng kết các kiến thức cần nhớ
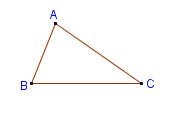
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_1.ggb Xem trực tiếp hình vẽ động trên màn hình. |
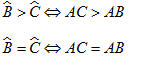
|
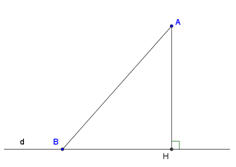
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_2.ggb Xem trực tiếp hình vẽ động trên màn hình. |
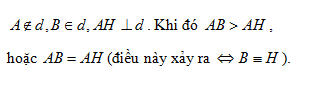
|
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_3.ggb Xem trực tiếp hình vẽ động trên màn hình. |
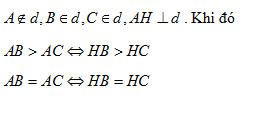
|
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_4.ggb Xem trực tiếp hình vẽ động trên màn hình. |
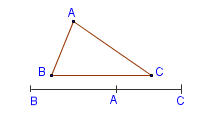
Với ba điểm bất kì, luôn có :
AB+AC>BC.
.
hoặc AB+AC=BC (điều này xảy ra <=>A nằm giữa và ).
|
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_5.ggb Xem trực tiếp hình vẽ động trên màn hình. |
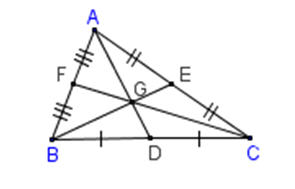
Trong tam giác ABC, ba đường trung tuyến AD,BE,CF đồng quy tại điểm G và 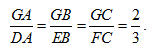
Điểm là trọng G tâm của tam giác ABC. |
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_6.ggb Xem trực tiếp hình vẽ động trên màn hình. |
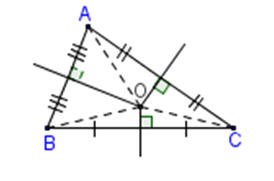
Trong tam giác ABC, ba đường phân giác đồng quy tại điểm I và điểm I cách đều ba cạnh :
IK=IL=IM:
|
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_7.ggb Xem trực tiếp hình vẽ động trên màn hình.
|
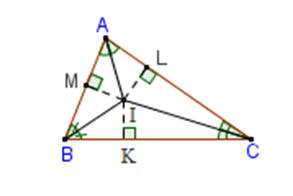
Trong tam giác ABC, ba đường trung trực đồng quy tại điểm O và điểm O cách đều ba đỉnh :
OA=OB=OC.
Điểm O là tâm đường tròn ngoại tiếp tam giác ABC
|
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_8.ggb Xem trực tiếp hình vẽ động trên màn hình. |
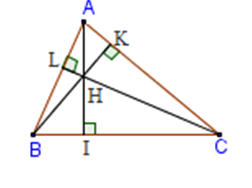
TRong tam giác ABC, ba đường cao AI,BK,CL đồng quy tại điểm H.
Điểm H là trực tâm của tam giác ABC.
|
Tải trực tiếp tệp hình học động: L7_Ch3_tamgiac_9.ggb Xem trực tiếp hình vẽ động trên màn hình. |
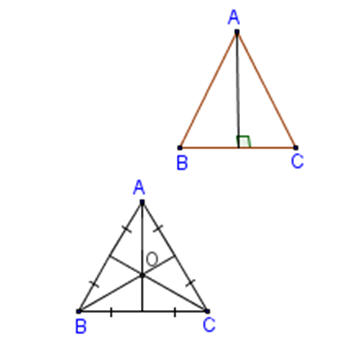
Tam giác ABC cân tại A<=> Hai trong bốn đường sau trùng nhau : đường trung trực của cạnh BC, đường trung tuyến, đường cao và đường phân giác cùng xuất phát từ đỉnh A (từ đó, cả bốn đường trùng nhau).
Nếu tam giác ABC đều thì trọng tâm, trực tâm, điểm cách đều ba đỉnh và điểm (nằm trong tam giác) cách đều ba cạnh là bốn điểm trùng nhau. |
Câu hỏi ôn tập
1. Cho tam giác ABC. Hãy viết kết luận của hai bài toán sau về quan hệ giữa góc và cạnh đối diện trong một tam giác. 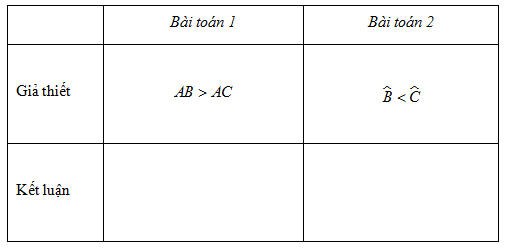
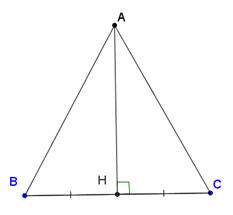
2. Từ điểm A không thuộc đường thẳng d, kẻ đường vuông góc AH, các đường xiên AB, AC đến đường thẳng d. Hãy điền dấu (>,<) vào các chỗ trống (…) dưới đây cho đúng :
a) AB …… AH ; AC …… AH.
b) Nếu HB …… HC thì AB …… AC.
c) Nếu AB …… AC thì HB …… HC.
3. Cho tam giác DEF. Hãy viết các bất đẳng thức về quan hệ giữa các cạnh của tam giác này.
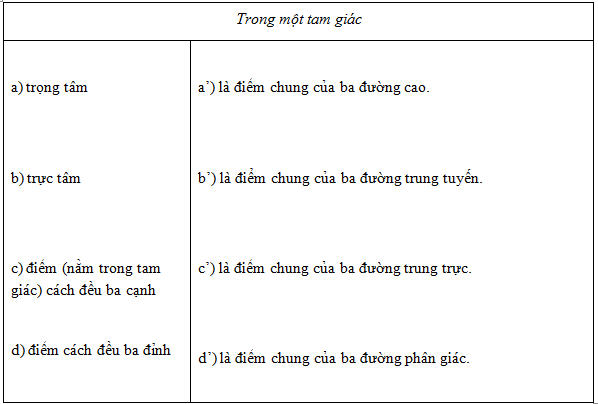
4. Hãy ghép đôi hai ý ở hai cột để được khẳng định đúng 
5. Cũng với yêu cầu như ở câu 4
6. a) Hãy nêu tính chất của trọng tâm của một tam giác : các cách xác định trọng tâm.
b) Bạn Nam nói : “Có thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác”. Bạn Nam nói đúng hay sai ? Tại sao ?
7. Những tam giác nào có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao ?
8. Những tam giác nào có trọng tâm đồng thời là trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh ? Bài tập 63. Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB.
Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE.
a) Hãy so sánh góc ADC và góc AEB.
b) Hãy so sánh các đoạn thẳng AD và AE.
64. Gọi MH là đường cao của tam giác MNP. Chứng minh rằng : Nếu MN < MP thì HN < HP và 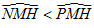 (yêu cầu xét hai trường hợp : khi góc N nhọn và khi góc N tù). (yêu cầu xét hai trường hợp : khi góc N nhọn và khi góc N tù).
65. Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài như sau : 1cm, 2cm, 3cm, 4cm và 5cm ?
66. Đố : Bốn điểm dân cư được xây dựng như hình 58. Hãy tìm vị trí đặt một nhà máy sao cho tổng các khoảng cách từ nhà máy đến bốn điểm dân cư này là nhỏ nhất. 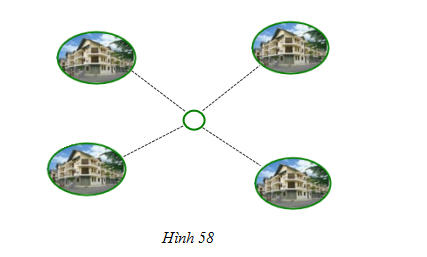
Tải trực tiếp tệp hình học động:L7_Ch3_h58.ggb
Xem trực tiếp hình vẽ động trên màn hình. 67. Cho tam giác MNP với đường trung tuyến MR và trọng tâm Q.
a) Tính tỉ số các diện tích của hai tam giác MPQ và RPQ.
b) Tính tỉ số các diện tích của hai tam giác MNQ và RNQ.
c) So sánh các diện tích của hai tam giác RPQ và RNQ.
Từ các kết quả trên, hãy chứng minh các tam giác QMN, QNP, QPM có cùng diện tích.
68. Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy.
a) Hãy tìm điểm M cách đều hai cạnh của góc xOy và cách đều hai điểm A, B.
b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a ?
69. Cho hai đường thẳng phân biệt không song song, không vuông góc a và b, điểm M không nằm trên hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
70. Cho A, B là hai điểm phân biệt và d là đường trung trực của đoạn thẳng AB.
a) Ta kí hiệu PA là nửa mặt phẳng bờ d có chứa điểm A (không kể đường thẳng d). Gọi N là một điểm của PA và M là giao điểm của đường thẳng NB và d. Hãy so sánh NB với NM + MA ; từ đó suy ra NA < NB.
b) Ta kí hiệu PB là nửa mặt phẳng bờ d có chứa điểm B (không kể d). Gọi N’ là một điểm của PB . Chứng minh rằng N’B < N’A.
c) Gọi L là một điểm sao cho LA < LB. Hỏi điểm L nằm ở đâu, trong PA , PB hay trên d ?
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng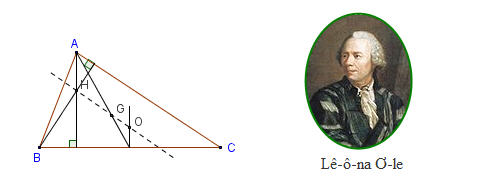

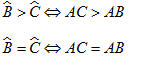

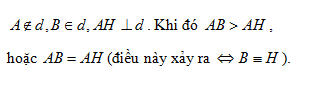

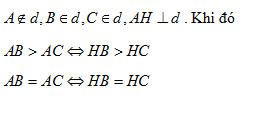


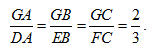







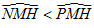 (yêu cầu xét hai trường hợp : khi góc N nhọn và khi góc N tù).
(yêu cầu xét hai trường hợp : khi góc N nhọn và khi góc N tù). 


