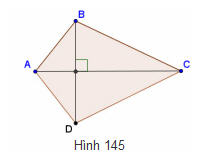
Tải trực tiếp tệp hình học động: L8_Ch2_h145.ggb Xem trực tiếp hình vẽ động trên màn hình.
Gợi ý. SABC = … SADC = … SABCD = …
2. Công thức tính diện tích hình thoi
 Hãy viết công thức tính diện tích hình thoi theo hai đường chéo.
Gợi ý. Hình thoi có hai đường chéo vuông góc.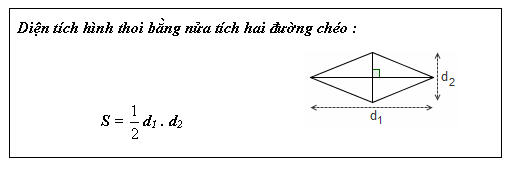 
 Hãy tính diện tích hình thoi bằng cách khác.
Gợi ý. Hình thoi cũng là hình bình hành.
3. Ví dụ
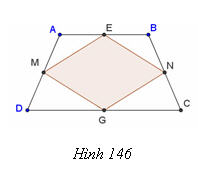
Tải trực tiếp tệp hình học động: L8_Ch2_h146.ggb Xem trực tiếp hình vẽ động trên màn hình.
Trong một khu vườn hình thang cân ABCD (đáy nhỏ AB = 30m, đáy lớn CD = 50m, diện tích bằng 800m2), người ta làm một bồn hoa hình tứ giác MENG với M, E, N, G là trung điểm các cạnh của hình thang cân. (h. 146). a) Tứ giác MENG là hình gì ? b) Tính diện tích của bồn hoa. Giải. (h. 147)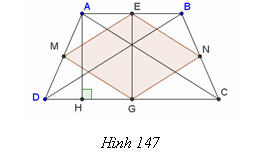 
Tải trực tiếp tệp hình học động: L8_Ch2_h147.ggb Xem trực tiếp hình vẽ động trên màn hình.
a) Ta có ME // BD và ME =1/2 BD, GN // BD và GN = 1/2 BD. Suy ra: ME // GN và Me = GN = 1/2 BD. Vậy MENG là hình bình hành. Tương tự, ta có EN // MG và EN = MG = 1/2 AC. Mặt khác, ta có BD = AC (hai đường chéo của hình thang cân), suy ra: ME = GN = EN = MG, từ đó MENG là hình thoi. b) MN là đường trung bình của hình thang, nên: MN = (AB + CD)/2 = (30 + 58)/2 = 40 (m). EG là đường cao của hình thang nên MN . EG = 800, suy ra: EG = 800/40 = 20(m). Diện tích bồn hoa hình thoi là : 1/2 MN . EG = 1/2 . 40 . 20 = 400 (m2).
BÀI TẬP
32. a) Hãy vẽ một tứ giác có độ dài hai đường chéo là : 3,6cm ; 6cm và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy ? Hãy tính diện tích mỗi tứ giác vừa vẽ. b) Hãy tính diện tích hình vuông có độ dài đường chéo là d. 33. Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi. 34. Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi ? So sánh diện tích hình thoi và diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi. 35. Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 600. 36. Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn ? Vì sao ?
School@net
|
Tìm kiếm
Xem giỏ hàng
Khách: 4
Thành viên: 0
Tổng cộng: 4
Hãy tính diện tích tứ giác ABCD theo AC, BD, biết AC vuông góc với BD tại H (h. 145).
