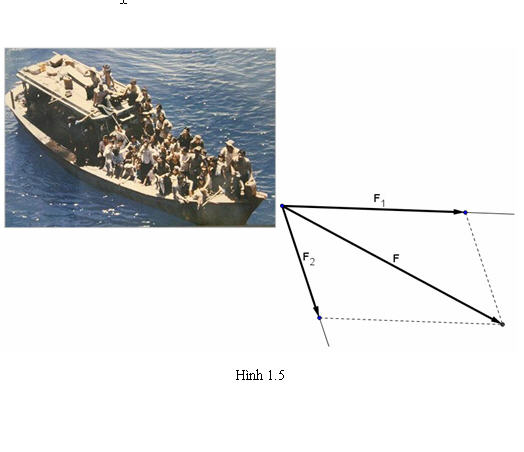
Tải trực tiếp tệp hình học động:L10_Ch1_h1.5.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Định nghĩa

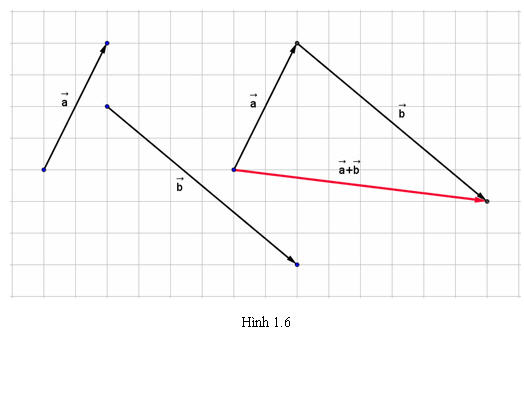
Tải trực tiếp tệp hình học động:L10_Ch1_h1.6.ggb
Xem trực tiếp hình vẽ động trên màn hình.
2. Quy tắc hình bình hành
Nếu là hình bình hành thì 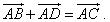
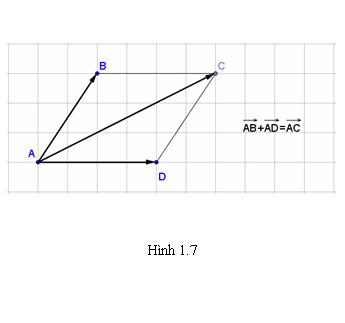
Tải trực tiếp tệp hình học động:L10_Ch1_h1.7.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Trên hình 1.5, hợp lực của hai lực 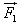 và và 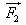 là lực là lực 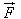 được xác định bằng quy tắc hình bình hành. được xác định bằng quy tắc hình bình hành.
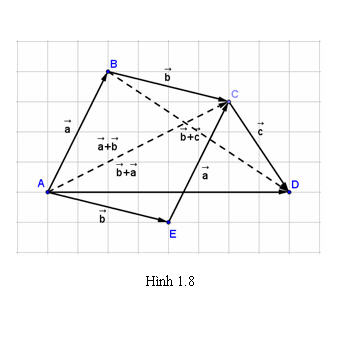
3. Tính chất của phép cộng các vectơ

Hình 1.8 minh họa cho các tính chất trên.
Tải trực tiếp tệp hình học động:L10_Ch1_h1.8.ggb
Xem trực tiếp hình vẽ động trên màn hình.
?1. Hãy kiểm tra các tính chất của phép cộng trên hình 1.8.
4. Hiệu của hai vectơ

a) Vectơ đối

Ví dụ 1. Nếu lần lượt là trung điểm của các cạnh của tam giác (h.1.9), khi đó ta có:
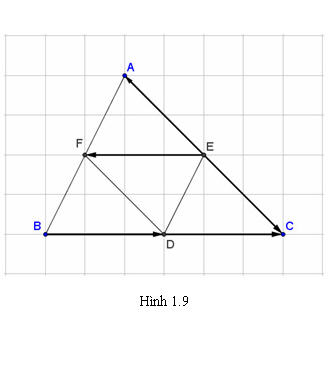
Tải trực tiếp tệp hình học động:L10_Ch1_h1.9.ggb
Xem trực tiếp hình vẽ động trên màn hình.
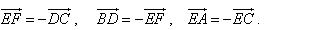
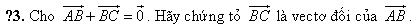
b) Định nghĩa hiệu của hai vectơ
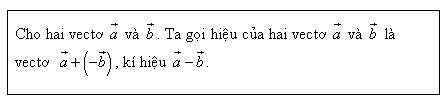
Như vậy:
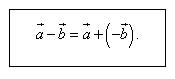
Từ định nghĩa hiệu của hai vectơ, suy ra:
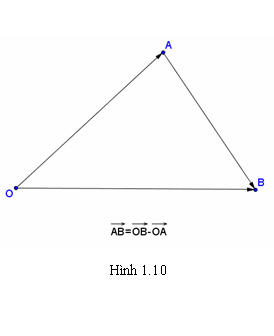
Tải trực tiếp tệp hình học động:L10_Ch1_h1.10.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Với ba điểm tùy ý ta có:
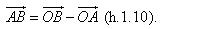
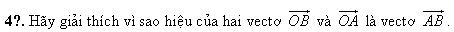
Chú ý. 1) Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ. 2) Với ba điểm tùy ý ta luôn có: 
Thực chất hai quy tắc trên được suy ra từ phép cộng vectơ. Ví dụ 2. Với bốn điểm bất kì ta luôn có: 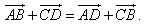
Thật vậy, lấy một điểm tùy ý ta có: 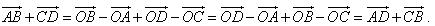
5. Áp dụng
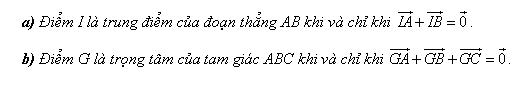
Chứng minh:
Tải trực tiếp tệp hình học động:L10_Ch1_h1.11.ggb
Xem trực tiếp hình vẽ động trên màn hình.
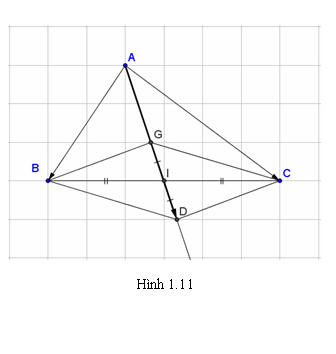
b) Trọng tâm G của tam giác ABC nằm trên trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Khi đó là hình bình hành và là trung điểm của đoạn thẳng .
Suy ra: 
Do đó ba điểm thẳng hàng, , điểm nằm giữa và . Vậy là trọng tâm của tam giác .
Câu hỏi và bài tập
1. Cho đoạn thẳng và điểm nằm giữa và sao cho . Vẽ các vectơ: 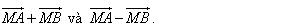
2. Cho hình bình hành và một điểm tùy ý. Chứng minh rằng: 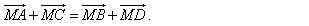
3. Chứng minh rằng đối với tứ giác bất kì ta luôn có: 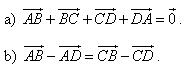
4. Cho tam giác . Bên ngoài của tam giác vẽ các hình bình hành . Chứng minh rằng: 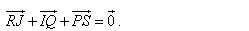
5. Cho tam giác đều cạnh bằng . Tính độ dài của các vectơ : 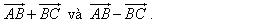
6. Cho hình bình hành có tâm . Chứng minh rằng: 
Bài đọc thêm
Thuyền buồm chạy ngược chiều gió

Thông thường người ta vẫn nghĩ rằng gió thổi về hướng nào thì sẽ đẩy thuyền buồm về hướng đó. Trong thực tế con người đã nghiên cứu tìm cách lợi dụng sức gió làm cho thuyền buồm chạy ngược chiều gió. Vậy người ta đã làm như thế nào để thực hiện được điều tưởng chừng như vô lí đó? Nói một cách chính xác thì người ta có thể làm cho thuyền chuyển động theo một góc nhọn, gần bằng 1/2 góc vuông đối với chiều gió thổi. Chuyển động này được thực hiện theo đường dích dắc nhằm tới hướng cần đến của mục tiêu. Để làm được điều đó ta đặt thuyền theo hướng và đặt buồm theo phương như hình vẽ.
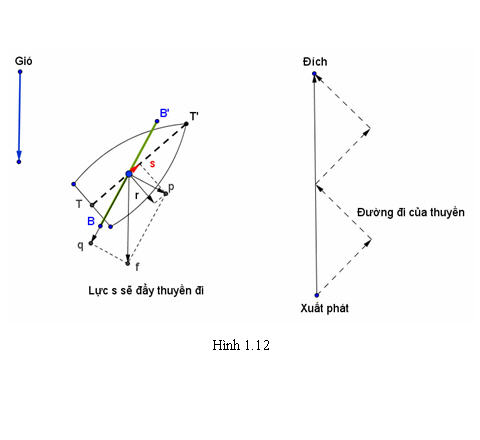
Tải trực tiếp tệp hình học động:L10_Ch1_h1.12.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Khi đó gió thổi tác động lên mặt buồm một lực. Tổng hợp lực là lực 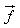 có điểm đặt ở chính giữa buồm. Lực có điểm đặt ở chính giữa buồm. Lực 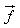 được phân tích thành hai lực: lực được phân tích thành hai lực: lực 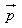 vuông góc với cánh buồm và lực vuông góc với cánh buồm và lực 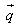 theo chiều dọc cánh buồm. Ta có theo chiều dọc cánh buồm. Ta có 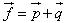 . Lực . Lực 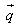 này không đẩy buồm đi đâu cả vì lực cản của gió đối với buồm không đáng kể. Lúc đó chỉ còn lực này không đẩy buồm đi đâu cả vì lực cản của gió đối với buồm không đáng kể. Lúc đó chỉ còn lực 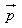 đẩy buồm dưới một góc vuông. Như vậy khi có gió thổi, luôn luôn có một lực đẩy buồm dưới một góc vuông. Như vậy khi có gió thổi, luôn luôn có một lực 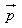 vuông góc với mặt phẳng của buồm. Lực vuông góc với mặt phẳng của buồm. Lực 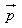 này được phân tích thành lực này được phân tích thành lực 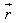 vuông góc với sống thuyền và lực vuông góc với sống thuyền và lực 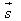 dọc theo sống thuyền hướng về mũi thuyền. Khi đó ta có dọc theo sống thuyền hướng về mũi thuyền. Khi đó ta có 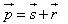 . Lực . Lực 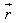 rất nhỏ so với sức cản rất lớn của nước, do thuyền buồm có sống thuyền rất sâu. Chỉ còn lực rất nhỏ so với sức cản rất lớn của nước, do thuyền buồm có sống thuyền rất sâu. Chỉ còn lực 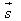 hướng về phía trước dọc theo sống thuyền đẩy thuyền đi một góc nhọn ngược với chiều gió thổi. Bằng cách đổi hướng thuyền theo con đường dích dắc, thuyền có thể đi tới đích theo hướng ngược chiều gió mà không cần lực đẩy. hướng về phía trước dọc theo sống thuyền đẩy thuyền đi một góc nhọn ngược với chiều gió thổi. Bằng cách đổi hướng thuyền theo con đường dích dắc, thuyền có thể đi tới đích theo hướng ngược chiều gió mà không cần lực đẩy.
schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng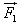 và
và 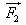 . Hai lực
. Hai lực 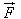 là tổng của hai lực
là tổng của hai lực 


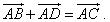






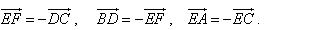
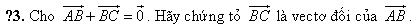
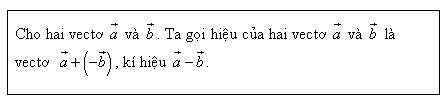
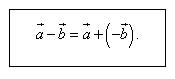

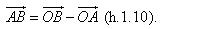
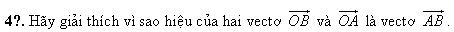

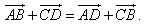
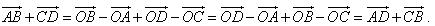
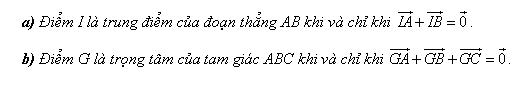


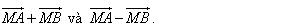
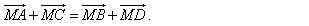
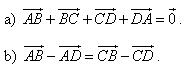
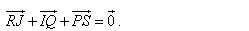
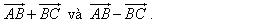



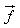 có điểm đặt ở chính giữa buồm. Lực
có điểm đặt ở chính giữa buồm. Lực 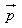 vuông góc với cánh buồm và lực
vuông góc với cánh buồm và lực 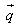 theo chiều dọc cánh buồm. Ta có
theo chiều dọc cánh buồm. Ta có 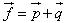 . Lực
. Lực 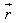 vuông góc với sống thuyền và lực
vuông góc với sống thuyền và lực 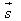 dọc theo sống thuyền hướng về mũi thuyền. Khi đó ta có
dọc theo sống thuyền hướng về mũi thuyền. Khi đó ta có 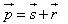 . Lực
. Lực 

