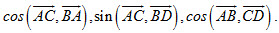Trong chương trình này chúng ta sẽ nghiên cứu thêm một phép toán mới về vecto, đó là phép nhân vô hướng của hai vecto. Phép nhân này cho kết quả là một số, số đó gọi là tích vô hướng của hai vecto. Để có thể xác định tích vô hướng của hai vecto ta cần đến khái niệm giá trị lượng giác của một góc α bất kì với 0o ≤ ≤ 180o là mở rộng của khái niệm tỉ số lượng giác của một góc nhọn α đã biết ở lớp 9.
BÀI 1. Giá trị lượng giác của một góc bất kì
từ 0o đến 180o
1Tam giác ABC vuông tại A có góc nhọn 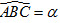 . Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn đã học ở lớp 9. . Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn đã học ở lớp 9.
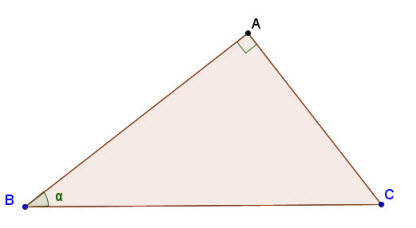
Hình 2.1
Tải trực tiếp tệp hình học động:L10_cb_Ch2_h2.1.ggb Xem trực tiếp hình vẽ động trên màn hình.
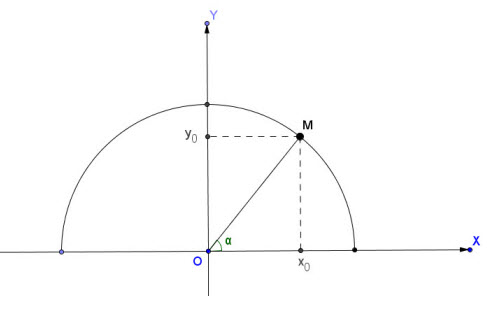
2Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R=1 được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn thì ta có thể
xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho 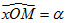 . Giả sử điểm M có tọa độ (x0;y0). . Giả sử điểm M có tọa độ (x0;y0).
Hình 2.2
Tải trực tiếp tệp hình học động:L10_cb_Ch2_h2.2.ggb Xem trực tiếp hình vẽ động trên màn hình.
Mở rộng khái niệm tỉ số lượng giác đối với góc nhọn cho những góc bất kì với 0o ≤ ≤ 180o, ta có định nghĩa sau đây:
1. Định nghĩa
Với một góc (0o ≤ ≤ 180o) ta xác định một điểm M trên nửa đường tròn đơn vị (h.2.3) sao cho 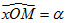 và giả sử điểm M có tọa độ M(x0;y0). Khi đó ta định nghĩa: và giả sử điểm M có tọa độ M(x0;y0). Khi đó ta định nghĩa:

Hình 2.3
Tải trực tiếp tệp hình học động:L10_cb_Ch2_h2.3.ggb Xem trực tiếp hình vẽ động trên màn hình.
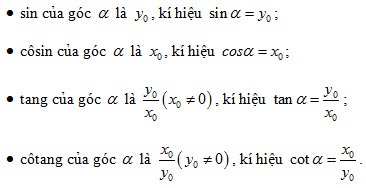
Các số sin, cos, tan, cot được gọi là các giá trị lượng giác của góc .
Ví dụ. Tìm các giá trị lượng giác của góc 1350.

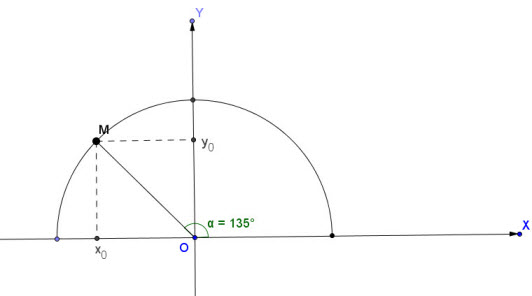
Hình 2.4
Tải trực tiếp tệp hình học động:L10_cb_Ch2_h2.4.ggb Xem trực tiếp hình vẽ động trên màn hình.
Chú ý.
+ Nếu là góc tù thì cos < 0, tan < 0, cot < 0.
+ tan chỉ xác định khi , cot chỉ xác định khi và .
2. Tính chất
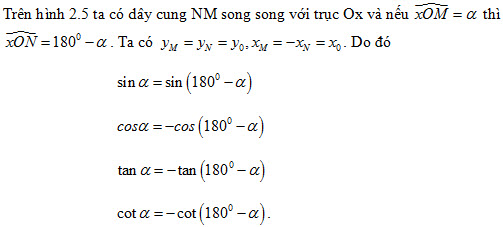
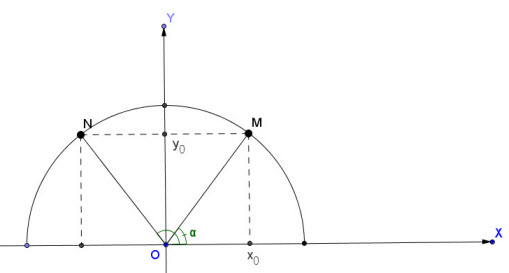
Hình 2.5
Tải trực tiếp tệp hình học động:L10_cb_Ch2_h2.5.ggb Xem trực tiếp hình vẽ động trên màn hình.
3. Giá trị lượng giác của các góc đặc biệt
Giá trị lượng giác của các góc bất kì có thể tìm thấy trên bảng số hoặc trên máy tính bỏ túi.
Sau đây là giá trị lượng giác của một số góc đặc biệt mà chúng ta cần ghi nhớ.
Bảng giá trị lượng giác của các góc đặc biệt
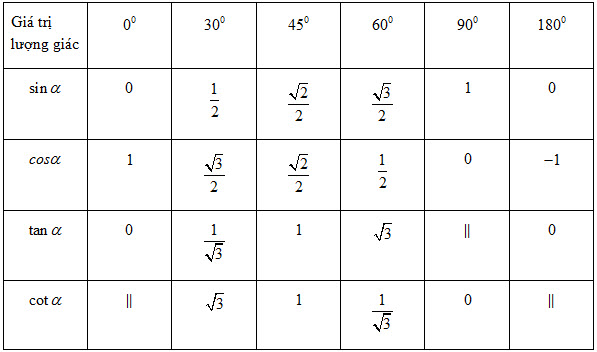
Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.
Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác.
Chẳng hạn:
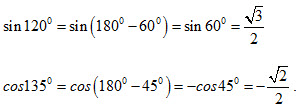
3Tìm các giá trị lượng giác của các góc 1200, 1500.
4. Góc giữa hai vectơ
a) Định nghĩa

b) Chú ý. Từ định nghĩa ta có 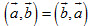 . .
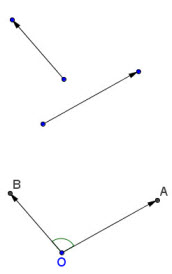
Hình 2.6
Tải trực tiếp tệp hình học động:L10_cb_Ch2_h2.6.ggb Xem trực tiếp hình vẽ động trên màn hình.
4Khi nào góc giữa hai vectơ bằng 00 ? Khi nào góc giữa hai vectơ bằng 1800 ?
c) Ví dụ. Cho tam giác ABC vuông tại A và có góc 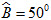 (h.2.7). Khi đó: (h.2.7). Khi đó:
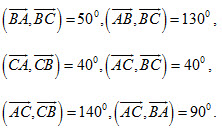
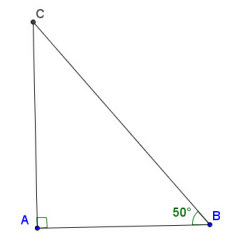
Hình 2.7
Tải trực tiếp tệp hình học động:L10_cb_Ch2_h2.7.ggb Xem trực tiếp hình vẽ động trên màn hình.
5. Sử dụng máy tính bỏ túi để tính giá trị lượng giác của một góc
Ta có thể sử dụng các loại máy tính bỏ túi để tính giá trị lượng giác của một góc, chẳng hạn đối với máy CASIO fx – 500MS cách thực hiện như sau:
a) Tính các giá trị lượng giác của góc
Sau khi mở máy ấn phím 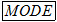 nhiều lần để màn hình hiện lên dòng chữ ứng với các số sau đây: nhiều lần để màn hình hiện lên dòng chữ ứng với các số sau đây:
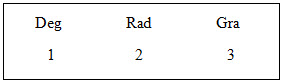
Sau đó ấn phím 1 để xác định đơn vị đo góc là “độ” và tính giá trị lượng giác của góc.
- Tính sin, cos và tan.
Ví dụ 1. Tính sin63052’41”.
Ấn liên tiếp các phím sau đây:
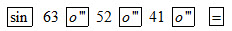
Ta được kết quả là: sin63052’41” ≈ 0,897859012.
Để tính cos và tan ta cũng làm như trên, chỉ thay việc ấn phím sin bằng phím cos hay tan.
b) Xác định độ lớn của góc khi biết giá trị lượng giác của góc đó
Sau khi mở máy và chọn đơn vị đo góc, để tính góc khi biết các giá trị lượng giác của góc đó ta làm như ví dụ sau.
Ví dụ 2. Tìm x biết sinx = 0,3502.
Ta ấn liên tiếp các phím sau đây:
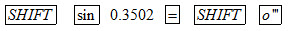
và được kết quả là : x ≈ 20029’58”.
Muốn tìm x khi biết cosx, tanx ta làm tương tự như trên, chỉ thay phím sin bằng phím cos, tan.
Câu hỏi và bài tập
1. Chứng minh rằng trong tam giác ABC ta có:
a) sinA = sin(B + C)
b) cosA = - cos(B + C).
2. Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử 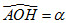 . Tính AK và OK theo a và . . Tính AK và OK theo a và .
3. Chứng minh rằng :
a) sin1050 = sin750;
b) cos1700 = - cos100;
c) cos1220 = - cos580.
4. Chứng minh rằng với mọi góc (0o ≤ ≤ 180o) ta đều có cos2 + sin2 = 1.
5. Cho góc , với  . Tính giá trị của biểu thức: P = 3sin2x + cos2 . Tính giá trị của biểu thức: P = 3sin2x + cos2
6. Cho hình vuông ABCD. Tính:
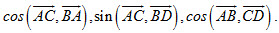
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng
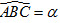 . Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn đã học ở lớp 9.
. Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn đã học ở lớp 9.
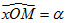 . Giả sử điểm M có tọa độ (x0;y0).
. Giả sử điểm M có tọa độ (x0;y0).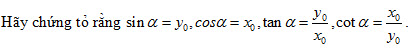


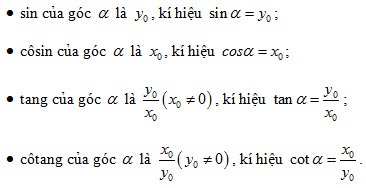


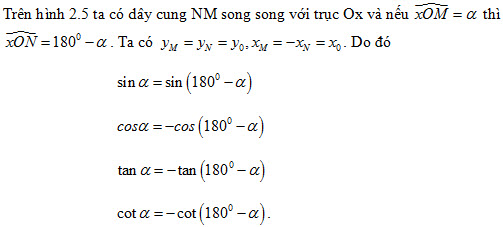


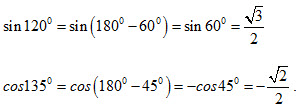

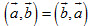 .
.
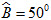 (h.2.7). Khi đó:
(h.2.7). Khi đó: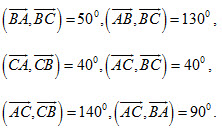

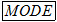 nhiều lần để màn hình hiện lên dòng chữ ứng với các số sau đây:
nhiều lần để màn hình hiện lên dòng chữ ứng với các số sau đây:
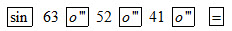
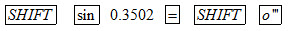
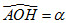 . Tính AK và OK theo a và .
. Tính AK và OK theo a và . . Tính giá trị của biểu thức: P = 3sin2x + cos2
. Tính giá trị của biểu thức: P = 3sin2x + cos2