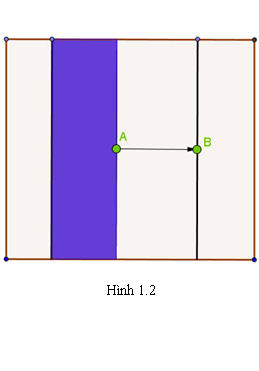
Tải trực tiếp tệp hình học động:L11_Ch1_h1.2.ggb
Xem trực tiếp hình vẽ động trên màn hình.
I. Định nghĩa
Trong mặt phẳng cho vectơ 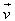 . Phép biến hình biến mỗi điểm M thành điểm M’ sao cho . Phép biến hình biến mỗi điểm M thành điểm M’ sao cho 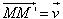 được gọi là phép tịnh tiến theo vectơ được gọi là phép tịnh tiến theo vectơ 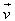 . . Phép tịnh tiến theo vectơ 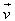 thường được ký hiệu là thường được ký hiệu là 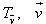 được gọi là vectơ tịnh tiến. được gọi là vectơ tịnh tiến.
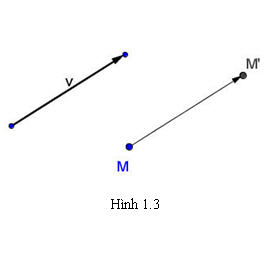
Tải trực tiếp tệp hình học động:L11_Ch1_h1.3.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Như vậy: 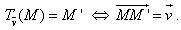
Phép tịnh tiến theo vectơ – không chính là phép đồng nhất. Ví dụ:
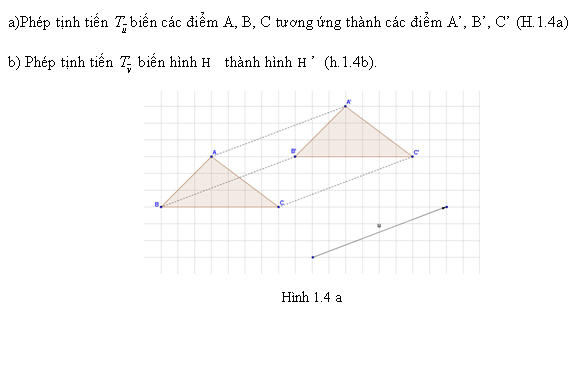
Tải trực tiếp tệp hình học động:L11_Ch1_h1.4a.ggb
Xem trực tiếp hình vẽ động trên màn hình.
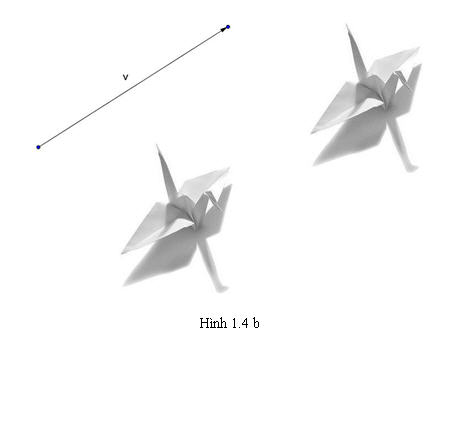
Tải trực tiếp tệp hình học động:L11_Ch1_h1.4b.ggb
Xem trực tiếp hình vẽ động trên màn hình.
?1. Cho hai tam giác đều ABE và BCD bằng nhau trên hình 1.5. Tìm phép tịnh tiến biến ba điểm A, B, E theo thứ tự thành ba điểm B, C, D.
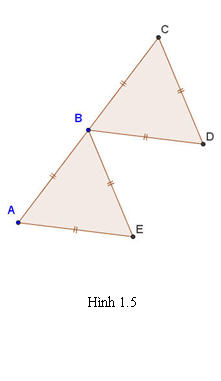
Tải trực tiếp tệp hình học động:L11_Ch1_h1.5.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Bạn có biết?
Vẽ những hình giống nhau có thể lát kín mặt phẳng là hứng thú của nhiều họa sĩ. Một trong những người nổi tiếng theo khuynh hướng đó là Mô-rit Cooc-ne-li Et-se (Maurits Cornelis Escher), họa sĩ người Hà Lan (1898 - 1972). Những bức tranh của ông được hàng triệu người trên thế giới ưa chuộng vì chẳng những rất đẹp mà còn chứa đựng những nội dung toán học sâu sắc. Sau đây là tranh của ông. 
II. Tính chất
Tính chất 1.
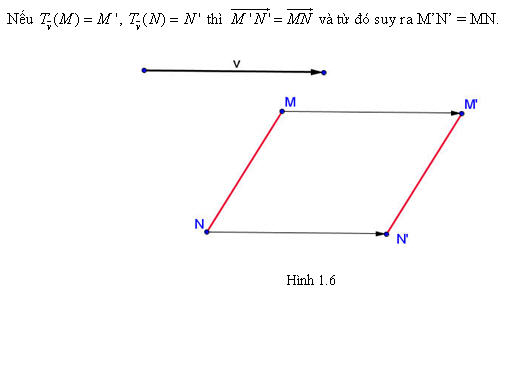
Tải trực tiếp tệp hình học động:L11_Ch1_h1.6.ggb
Xem trực tiếp hình vẽ động trên màn hình.
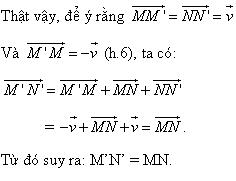
Nói cách khác, phép tính tiến bảo toàn khoảng cách giữa hai điểm bất kỳ. Từ tính chất 1 ta chứng minh được tính chất sau. Tính chất 2 Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính (h.1.7).
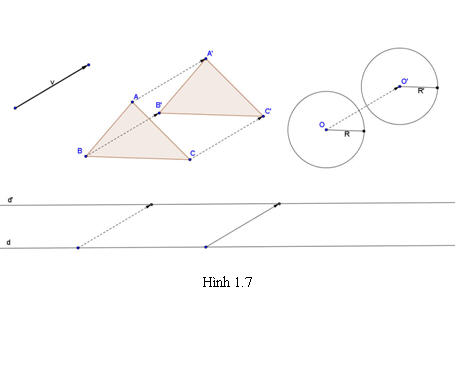
Tải trực tiếp tệp hình học động:L11_Ch1_h1.7.ggb
Xem trực tiếp hình vẽ động trên màn hình.
?2. Nêu cách xác định ảnh của đường thẳng d qua phép tịnh tiến theo vectơ 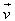 . .
III. Biểu thức tọa độ
Trong mặt phẳng tọa độ Oxy cho vectơ 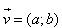 (h.1.8). (h.1.8). Với mỗi điểm M(x;y) ta có M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vectơ 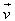 . .
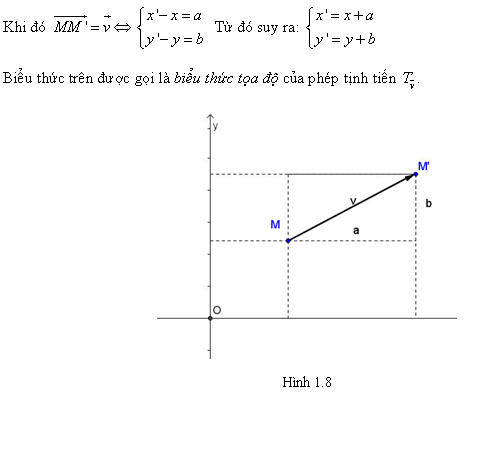
Tải trực tiếp tệp hình học động:L11_Ch1_h1.8.ggb
Xem trực tiếp hình vẽ động trên màn hình.
?3. Trong mặt phẳng tọa độ Oxy cho vectơ 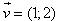 .Tìm tọa độ của điểm M’ là ảnh của điểm M(3; -1) qua phép tịnh tiến .Tìm tọa độ của điểm M’ là ảnh của điểm M(3; -1) qua phép tịnh tiến 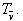 . .
Bài tập
1. Chứng minh rằng: 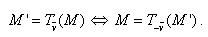
2. Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo vectơ 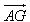 . . Xác định điểm D sao cho phép tịnh tiến theo vectơ 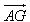 biến D thành A. biến D thành A. 3. Trong mặt phẳng tọa độ Oxy cho: Vectơ 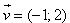 , hai điểm A(3; 5), B(-1;1) và đường thẳng d có phương trình x – 2y + 3 = 0. , hai điểm A(3; 5), B(-1;1) và đường thẳng d có phương trình x – 2y + 3 = 0. a. Tìm tọa độ của các điểm A’, B’ theo thứ tự là ảnh của A, B qua phép tịnh tiến theo 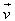 . . b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo 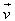 . . c. Tìm phương trình của đường thẳng d’ là ảnh của d qua phép tịnh tiến theo 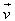 . . 4. Cho hai đường thẳng a và b song song với nhau. Hãy chỉ ra một phép tịnh tiến biến a thành b. Có bao nhiêu phép tịnh tiến như thế?
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng .
.
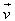 . Phép biến hình biến mỗi điểm M thành điểm M’ sao cho
. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho 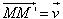 được gọi là phép tịnh tiến theo vectơ
được gọi là phép tịnh tiến theo vectơ 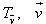 được gọi là vectơ tịnh tiến.
được gọi là vectơ tịnh tiến.
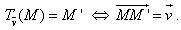





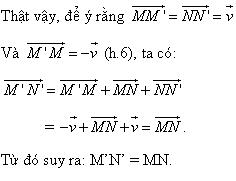

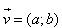 (h.1.8).
(h.1.8). 
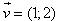 .Tìm tọa độ của điểm M’ là ảnh của điểm M(3; -1) qua phép tịnh tiến
.Tìm tọa độ của điểm M’ là ảnh của điểm M(3; -1) qua phép tịnh tiến 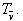 .
. 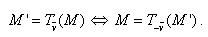
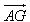 .
. 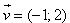 , hai điểm A(3; 5), B(-1;1) và đường thẳng d có phương trình x – 2y + 3 = 0.
, hai điểm A(3; 5), B(-1;1) và đường thẳng d có phương trình x – 2y + 3 = 0.

