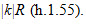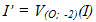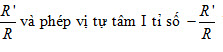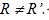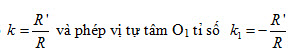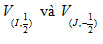
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.50.ggb Xem trực tiếp hình vẽ động trên màn hình. Phép vị tự tâm O, tỉ số k thường được kí hiệu là 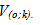 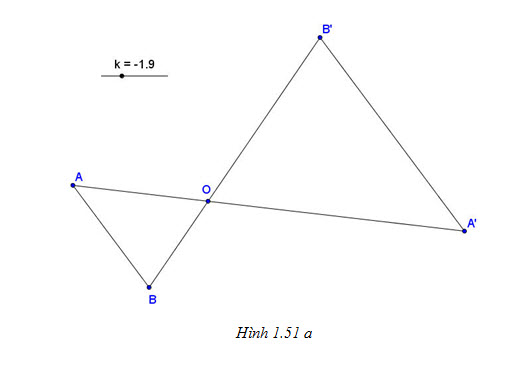
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.51a.ggb Xem trực tiếp hình vẽ động trên màn hình. 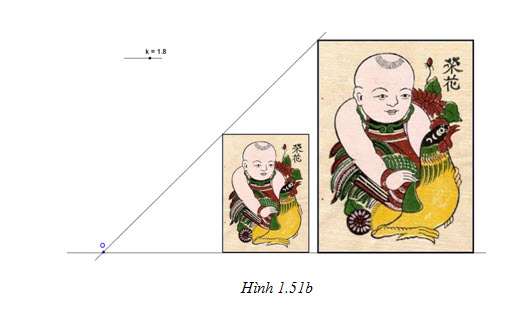
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.51b.ggb Xem trực tiếp hình vẽ động trên màn hình.
Ví dụ 1
a) Trên hình 1.51a các điểm A’, B’, O lần lượt là ảnh của các điểm A, B, O qua phép vị tự tâm O tỉ số -2.
b) Trong hình 1.51b phép vị tự tâm O, tỉ số 2 biến hình H thành hình H ’.
1. Cho tam giác ABC. Gọi E và F tương ứng là trung điểm AB và AC. Tìm một phép tự biến B và C tương ứng thành E và F.
Nhận xét
1) Phép vị tự biến tâm vị tự thành chính nó.
2) Khi k = 1, phép vị tự là phép đồng nhất
3) Khi k = -1, phép vị tự là phép đối xứng qua tâm vị tự.
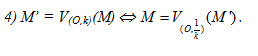
2. Chứng minh nhận xét 4
II. TÍNH CHẤT
Tính chất 1

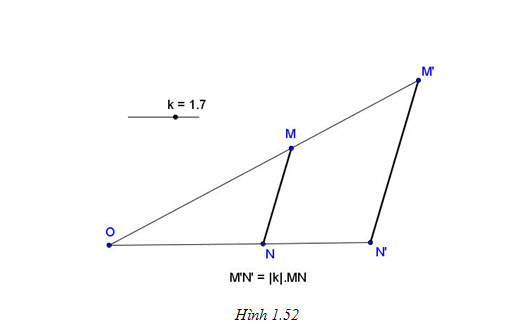
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.52.ggb Xem trực tiếp hình vẽ động trên màn hình. 
3. Để ý rằng: điểm B nằm giữa hai điểm A và C khi và chỉ khi 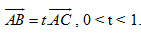 . .
Sử dụng ví dụ trên chứng minh rằng nếu điểm B nằm giữa hai điểm A và C thì điểm B’ nằm giữa hai điểm A’ và C’.
Tính chất 2
Phép vị tự tỉ số k:
a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy (h.1.53).
b)Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.
c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó (h.1.54).
d) Biến đường tròn bán kính R thành đường tròn bán kính 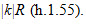 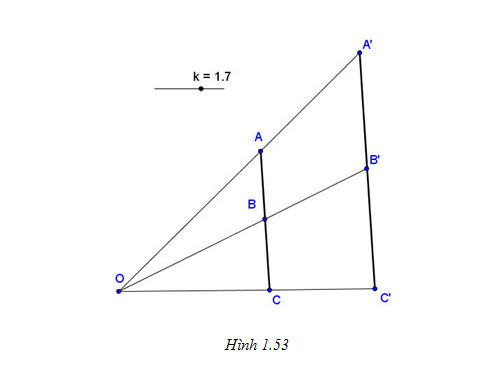
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.53.ggb Xem trực tiếp hình vẽ động trên màn hình. 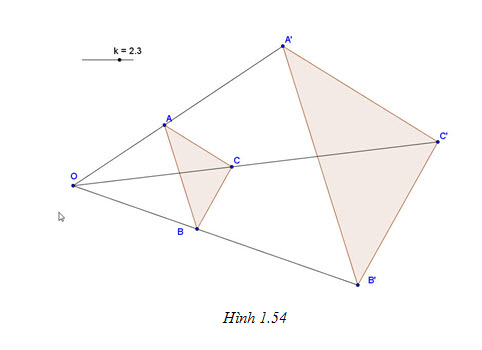
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.54.ggb Xem trực tiếp hình vẽ động trên màn hình. 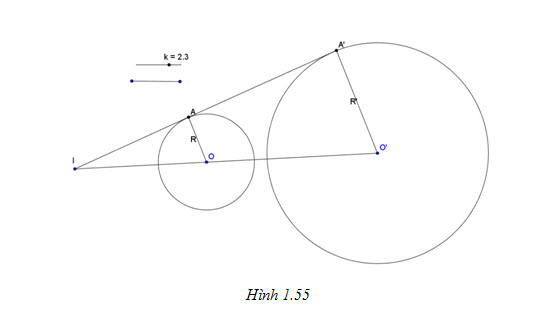
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.55.ggb Xem trực tiếp hình vẽ động trên màn hình. 4. Cho tam giác ABC có A’, B’, C’ theo thứ tự là trung điểm của các cạnh BC, CA, AB. Tìm một phép vị tự biến tam giác ABC thành tam giác A’B’C’ (h.1.56). 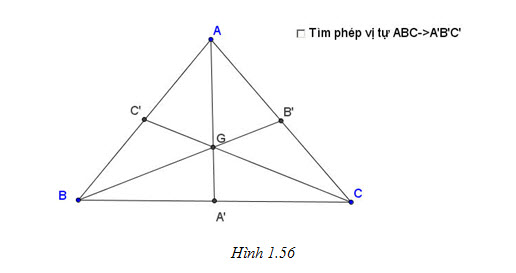
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.56.ggb Xem trực tiếp hình vẽ động trên màn hình. Ví dụ 3. Cho điểm O và đường tròn (I; R). Tìm ảnh của đường tròn đó qua phép vị tự tâm O tỉ số - 2. Giải Giải
Ta chỉ cần tìm 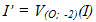
bằng cách lấy trên tia đối của tia OI điểm I’ sao cho OI’ = 2OI. Khi đó, ảnh của (I; R) là (I’; 2R) (h.1.57) 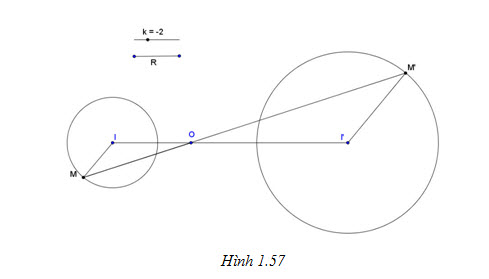
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.57.ggb Xem trực tiếp hình vẽ động trên màn hình. II. TÂM VỊ TỰ CỦA HAI ĐƯỜNG TRÒN
Ta đã biết phép vị tự biến đường tròn thành đường tròn. Ngược lại, ta có định lý sau:
Định lý
Với hai đường tròn bất kỳ luôn có một phép vị tự biến đường tròn này thành đường tròn kia.
Tâm của phép vị tự đó được gọi là tâm vị tự của hai đường tròn.
Cách tìm tâm vị tự của hai đường tròn
Cho hai đường tròn (I; R) và (I’;R’).
Có ba trường hợp xảy ra:
+ Trường hợp I trùng với I’
Khi đó, phép vị tự tâm I tỉ số 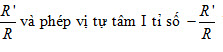
biến đường tròn (I; R) thành đường tròn (I; R’) (h.1.58). 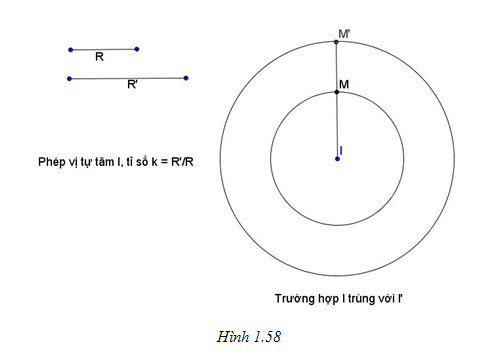
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.58.ggb Xem trực tiếp hình vẽ động trên màn hình. + Trường hợp I khác I’ và 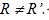
Lấy điếm M bất kỳ thuộc đường trong (I; R). đường thẳng qua I’ song song với IM cắt đường tròn (I’; R’) tại M’ và M’’. Giả sử M, M’ nằm cùng phía đối với đường thẳng II’ còn M, M’’ nằm khác phía đối với đường thẳng II’. Giả sử đường thẳng MM’ cắt đường thẳng II’ tại điểm O nằm ngoài đoạn thẳng II’, còn đường thẳng MM’’ cắt đường thẳng II’ tại điểm O1 nằm trong đoạn thẳng II’. 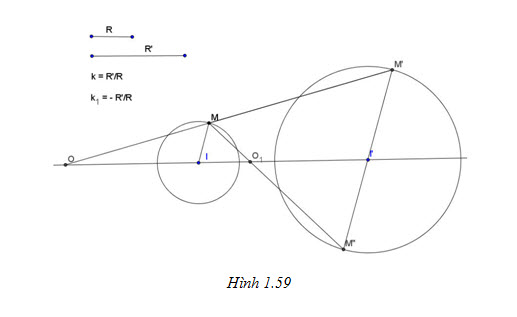
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.59.ggb Xem trực tiếp hình vẽ động trên màn hình.
Khi đó phép vị tự tâm O tỉ số 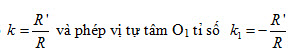
sẽ biến đường tròn (I; R) thành đường tròn (I’; R’). Ta gọi O là tâm vị tự ngoài còn O1 là tâm vị tự trong của hai đường tròn nói trên.
+ Trường hợp I khác I’ và R = R’.
Khi đó 
biến đường tròn (I;R) thành đường tròn (I’; R’). Nó chính là phép đối xứng tâm O1.
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.60.ggb Xem trực tiếp hình vẽ động trên màn hình. Ví dụ 4.
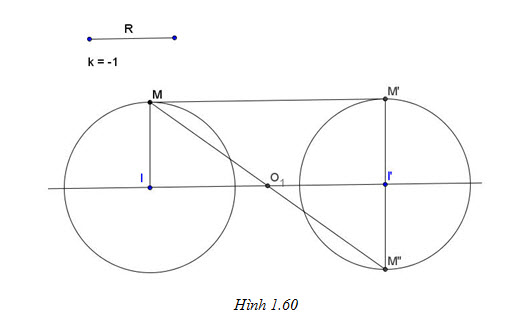
Cho hai đường tròn (O; 2R) và (O’; R) nằm ngoài nhau. Tìm phép vị tự biến (O; 2R) thành (O’; R). 
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.61.ggb Xem trực tiếp hình vẽ động trên màn hình.
Lấy điểm L bất kỳ trên đường tròn (O; 2R), đường thẳng qua O’, song song với OL cắt (O’; R) tại M và N (h.1.61). Hai đường thẳng LM và LN cắt đường thẳng OO’ lần lượt tại I và J. Khi đó các phép vị tự 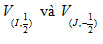
sẽ biến (O; 2R) thành (O’; R).
BÀI TẬP
1. Cho tam giác ABC có ba góc nhọn và H là trực tâm. Tìm ảnh của tam giác ABC qua phép vị tự tâm H, tỉ số 
2. Tìm tâm vị tự của hai đường tròn trong các trường hợp sau (h.1.62): 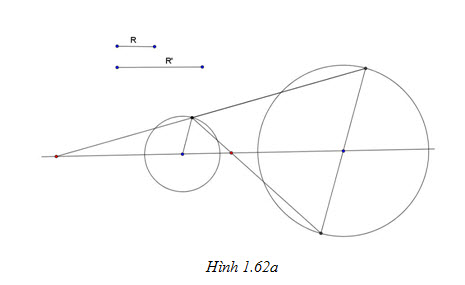
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.62.ggb Xem trực tiếp hình vẽ động trên màn hình. Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.62a.ggb Xem trực tiếp hình vẽ động trên màn hình. 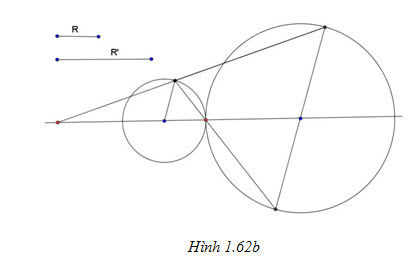
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.62b.ggb Xem trực tiếp hình vẽ động trên màn hình. 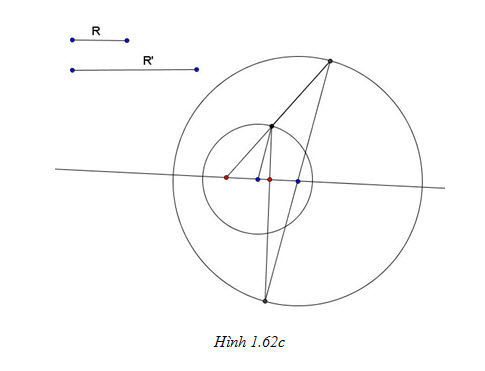
Tải trực tiếp tệp hình học động:L11cb_Ch1_h1.62c.ggb Xem trực tiếp hình vẽ động trên màn hình. 3. Chứng minh rằng khi thực hiện liên tiếp hai phép vị tự tâm O sẽ được một phép vị tự tâm O.
schoolnet
|

 Xem giỏ hàng
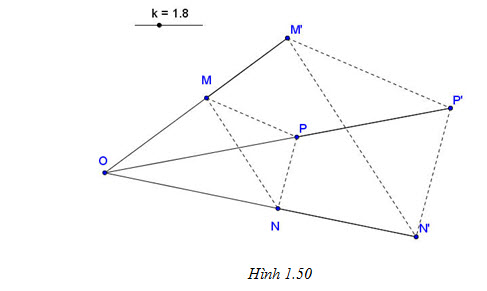
Xem giỏ hàng .Phép biến hình biến mỗi điểm M thành điểm M’ sao cho
.Phép biến hình biến mỗi điểm M thành điểm M’ sao cho 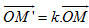 được gọi là phép vị tự tâm O, tỉ số k (h.1.50).
được gọi là phép vị tự tâm O, tỉ số k (h.1.50).
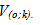


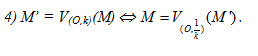



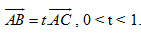 .
.