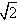Tải trực tiếp tệp hình học động:L11_Ch1_h1.63.ggb
Xem trực tiếp hình vẽ động trên màn hình.
I. Định nghĩa
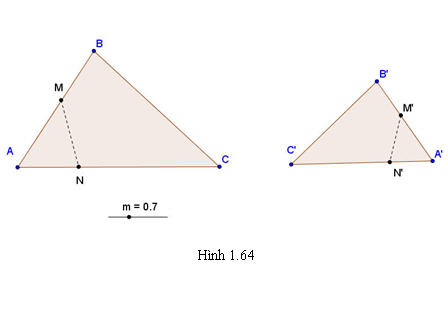
Định nghĩa Phép biến hình F được gọi là phép đồng dạng tỉ số k (k >0), nếu với hai điểm M, N bất kỳ và ảnh M’, N’ tương ứng của chúng ta luôn có M’N’ = k.MN (h.1.64).
Tải trực tiếp tệp hình học động:L11_Ch1_h1.64.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Nhận xét 1) Phép dời hình là phép đồng dạng tỉ số 1. 2) Phép vị tự tỉ số k là phép đồng dạng tử số |k|. ?1. Chứng minh nhận xét 2. 3) Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk. ?2. Chứng minh nhận xét 3. Ví dụ 1. Trong hình 1.65 phép vị tự tâm O tỉ số 2 biến hình  hành hình hành hình  . Phép đối xứng tâm I biến hình . Phép đối xứng tâm I biến hình 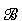 thành hình thành hình 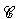 . Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép biến hình trên sẽ biến hình . Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép biến hình trên sẽ biến hình 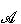 thành hình thành hình 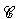 . .
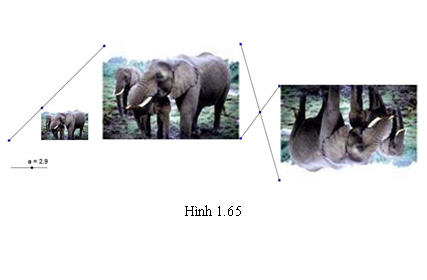
Tải trực tiếp tệp hình học động:L11_Ch1_h1.65.ggb
Xem trực tiếp hình vẽ động trên màn hình.
II. Tính chất
Phép đồng dạng tỉ số k: a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy. b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng. c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó. d) Biến đường tròn bán kính R thành đường tròn bán kính kR. ?3. Chứng minh tính chất a. ?4. Gọi A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’. Chú ý. Nếu một phép đồng dạng biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’ (h.1.66).
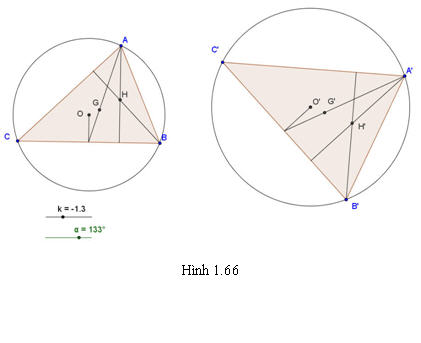
Tải trực tiếp tệp hình học động:L11_Ch1_h1.66.ggb
Xem trực tiếp hình vẽ động trên màn hình.
b) Phép đồng dạng biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thành đỉnh, biến cạnh thành cạnh.
III. Hình học
Chúng ta đã biết phép đồng dạng biến một tam giác thành tam giác đồng dạng với nó. Người ta cũng chứng minh được rằng cho hai tam giác đồng dạng với nhau thì luôn có một phép đồng dạng biến tam giác này thành tam giác kia. Vậy hai tam giác đồng dạng với nhau khi và chỉ khi có một phép đồng dạng biến tam giác này thành tam giác kia. Điều đó gợi cho ta cách định nghĩa các hình đồng dạng. Định nghĩa Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia. Ví dụ 2 a) Tam giác A’B’C’ là hình đồng dạng của tam giác ABC (h.1.67). b) Phép vị tự tâm I tỉ số 2 biến hình A thành hình B, phép quay tâm O góc 90 biến hình B thành hình C. Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép biến hình trên sẽ biến hình  thành hình thành hình  . Từ đó suy ra: hai hình . Từ đó suy ra: hai hình  và và đồng dạng với nhau. đồng dạng với nhau.
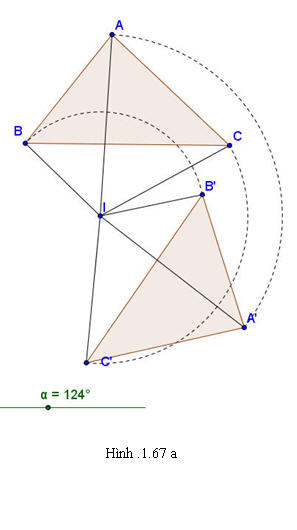
Tải trực tiếp tệp hình học động:L11_Ch1_h1.67a.ggb
Xem trực tiếp hình vẽ động trên màn hình.
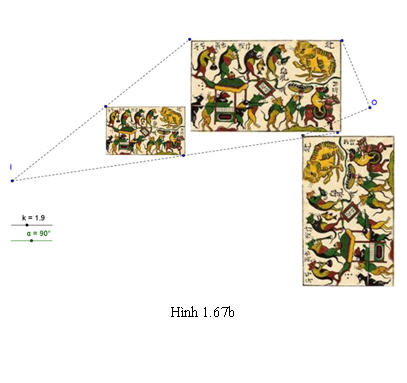
Tải trực tiếp tệp hình học động:L11_Ch1_h1.67b.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Ví dụ 3. Cho hình chữ nhật ABCD, AC tắt BD tại I. Goi H , K, L và lần lượt là trung điểm của AD, BC, KC, IX. Chứng minh rằng hai hình bình hành JLKI và IHAB đồng dạng với nhau. Giải: Gọi M là trung điểm của AB (h.1.68). Phép vị tự tâm C, tỉ số 2 biến hình thang JLKI thành hình thang IKBA. Phép đối xứng qua đường thẳng IM biến hình thang IKBA thành hình thang IHAB. Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép biến hình trên biến hình thang JLKI thành hình thang IHAB. Từ đó suy ra hai hình thang JLKI và IHAB đồng dạng với nhau.
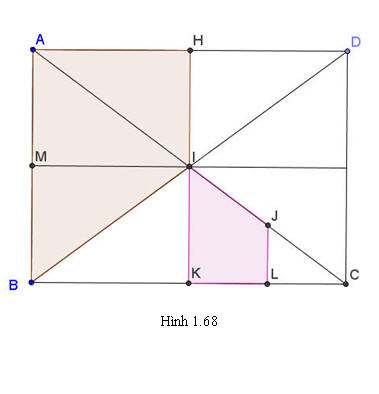
Tải trực tiếp tệp hình học động:L11_Ch1_h1.68.ggb
Xem trực tiếp hình vẽ động trên màn hình.
?5. Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau không?
Bài tập
1. Cho tam giác ABC. Xác định ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm B tỉ số 1/2 và phép đối xứng qua đường trung trực của BC. 2. Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hai hình thang JLKI và IHDC đồng dạng với nhau. 3. Trong mặt phẳng Oxy cho điểm I(1;1) và đường tròn tâm I bán kính 2. Viết phương trình của đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc 450 và phép vị tự tâm O, tỉ số 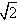 4. Cho tam giác ABC vuông góc tại A, AH là đường cao kẻ từ A. Tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC.
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng

 hành hình
hành hình  . Phép đối xứng tâm I biến hình
. Phép đối xứng tâm I biến hình 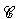 . Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép biến hình trên sẽ biến hình
. Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép biến hình trên sẽ biến hình