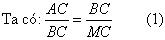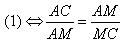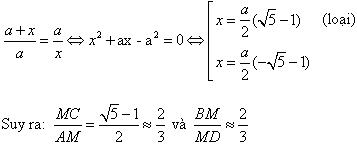
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.61.cg3
Xem trực tiếp hình vẽ động trên màn hình.
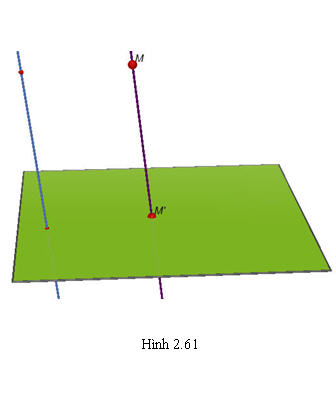
Mặt phẳng 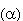 gọi là mặt phẳng chiếu. Phương gọi là mặt phẳng chiếu. Phương 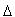 gọi là phương chiếu. gọi là phương chiếu. Phép đặt tương ứng mỗi điểm M trong không gian với hình chiếu M’ của nó trên mặt phẳng 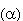 được gọi là phép chiếu song song lên được gọi là phép chiếu song song lên 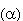 theo phương theo phương 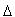 . . Nếu 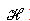 là một hình nào đó thì tập hợp là một hình nào đó thì tập hợp 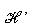 các hình chiếu M’ của tất cả những điểm M thuộc các hình chiếu M’ của tất cả những điểm M thuộc 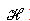 được gọi là hình chiếu của được gọi là hình chiếu của  qua phép chiếu song song nói trên. qua phép chiếu song song nói trên. Chú ý. Nếu một đường thẳng có phương trùng với phương chiếu thì hình chiếu của đường thẳng đó là một điểm. Sau đây, ta chỉ xét các chiếu của những đường thẳng có phương không trùng với phương chiếu.
II. Các tính chất của phép chiếu song song.
Định lí 1 a) Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó (h.2.62).
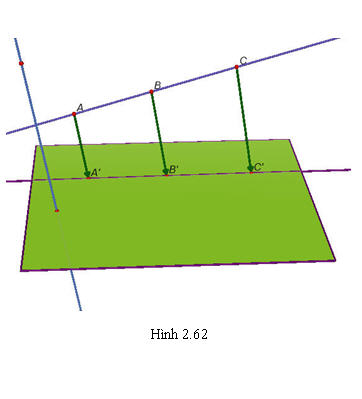
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.62.cg3
Xem trực tiếp hình vẽ động trên màn hình.
b) Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng. c) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau (h.2.63 và h.2.64).
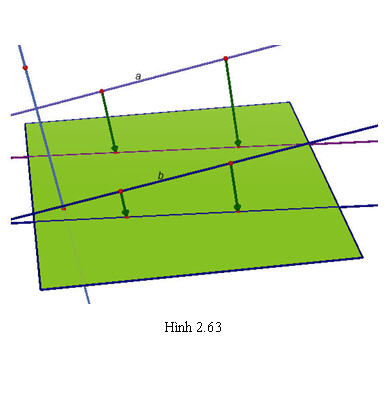
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.63.cg3
Xem trực tiếp hình vẽ động trên màn hình.
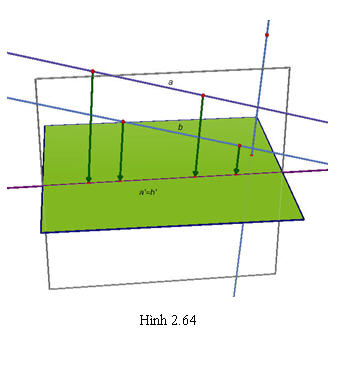
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.64.cg3
Xem trực tiếp hình vẽ động trên màn hình.
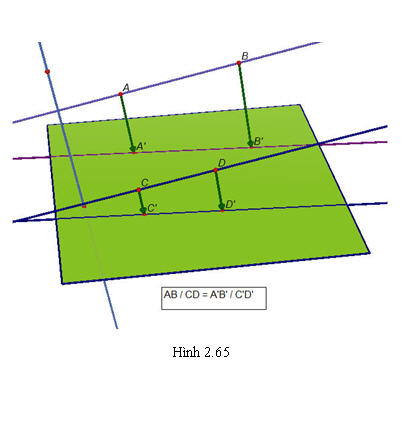
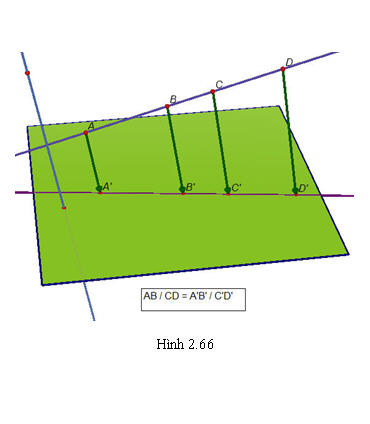
d) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng (h.2.65 và h.2.66).
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.65.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.66.cg3
Xem trực tiếp hình vẽ động trên màn hình.
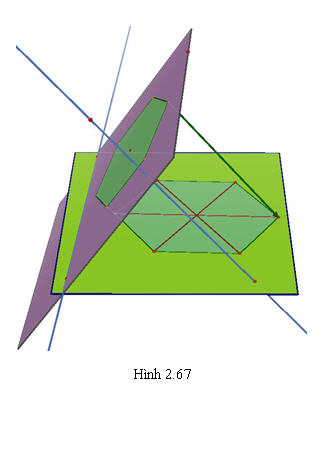
?1. Hình chiếu song song của một hình vuông có thể là hình bình hành được không? ?2. Hình 2.67 có thể là hình chiếu song song của hình lục giác đều được không? Tại sao?
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.67.cg3
Xem trực tiếp hình vẽ động trên màn hình.
III. Hình biểu diễn của một hình không gian trên mặt phẳng.
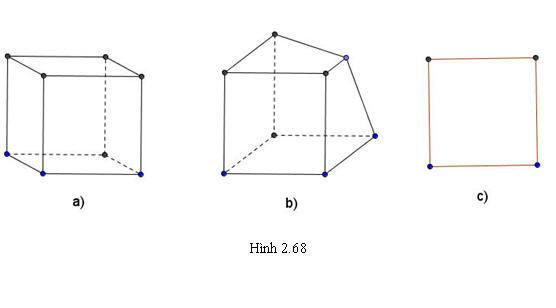
Hình biểu diễn của một hình H trong không gian là hình chiếu song song của hình H trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó. ?3. Trong các hình 2.68, hình nào biểu diễn cho hình lập phương?
Tải trực tiếp tệp hình học động:L11_Ch2_h2.68.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Hình biểu diễn của các hình thường gặp
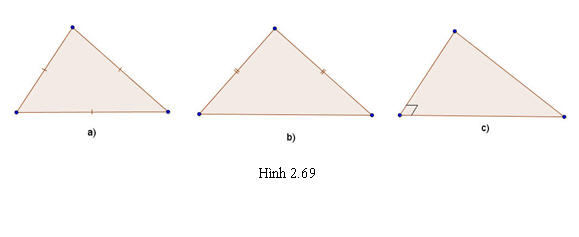
+ Tam giác. Một tam giác bất kì bao giờ cũng có thể coi là hình biểu diễn của một tam giác có dạng tùy ý cho trước (có thể là tam giác đều, tam giác cân, tam giác vuông,v.v…) (h.2.69)
Tải trực tiếp tệp hình học động :L11_Ch2_h2.69.ggb
Xem trực tiếp hình vẽ động trên màn hình.
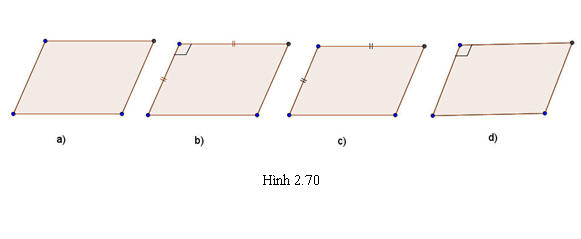
+ Hình bình hành. Một hình bình hành bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tùy ý cho trước (có thể là hình bình hành, hình vuông, hình thoi, hình chữ nhật…)(h.2.70).
Tải trực tiếp tệp hình học động :L11_Ch2_h2.70.ggb
Xem trực tiếp hình vẽ động trên màn hình.
+ Hình thang. Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang tùy ý cho trước, miễn là tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình thang ban đầu.
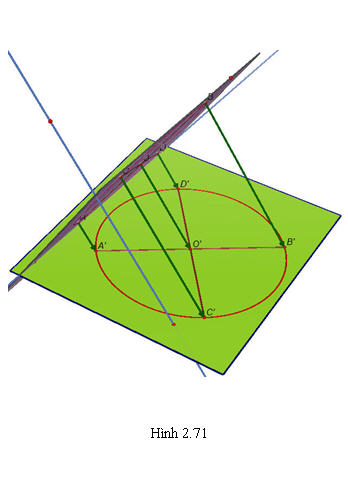
+ Hình tròn. Người ta thường dùng hình elip để biểu diễn cho hình tròn (h.2.71).
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.71.cg3
Xem trực tiếp hình vẽ động trên màn hình.
?4. Các hình 2.69a, 2.69b, 2.69c là hình biểu diễn của các tam giác nào?
?5. Các hình 2.70a, 2.70b, 2.70c, 2.70d là hình biểu diễn của các hình bình hành nào (hình bình hành, hình thoi, hình vuông, hình chữ nhật)? ?6. Cho hai mặt phẳng 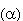 và và 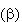 song song với nhau. Đường thẳng a cắt song song với nhau. Đường thẳng a cắt 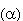 và và 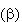 lần lượt tại A và C. Đường thẳng b song song với a cắt lần lượt tại A và C. Đường thẳng b song song với a cắt 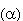 và và  lần lượt tại B và D. lần lượt tại B và D. Hình 2.72 minh họa nội dung nêu trên đúng hay sai?
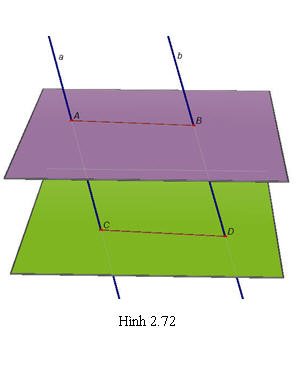
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save As):L11_Ch2_h2.72.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Bài đọc thêm
Cách biểu diễn ngũ giác đều
Một tam giác bất kì có thể coi là hình biểu diễn của một tam giác đều. Một hình bình hành có thể coi là hình biểu diễn của một hình vuông. Đối với ngũ giác đều, hình biểu diễn như thế nào?
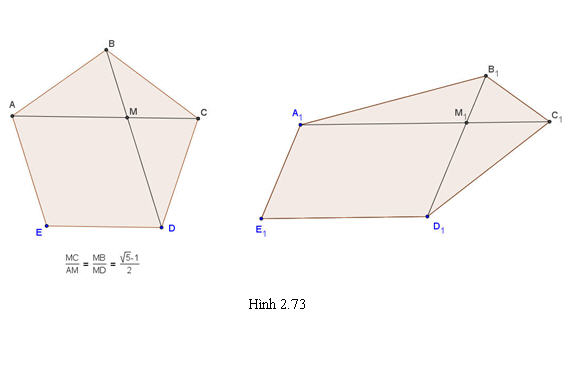
Giả sử ta có ngũ giác đều ABCDE với các đường chéo AC và BD cắt nhau ở điểm M (h.2.73). Ta nhận thấy hai tam giác ABC và BMC là đồng dạng (tam giác cân có chung góc C ở đáy. 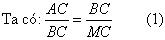
Tải trực tiếp tệp hình học động:L11_Ch2_h2.73.ggb
Xem trực tiếp hình vẽ động trên màn hình.
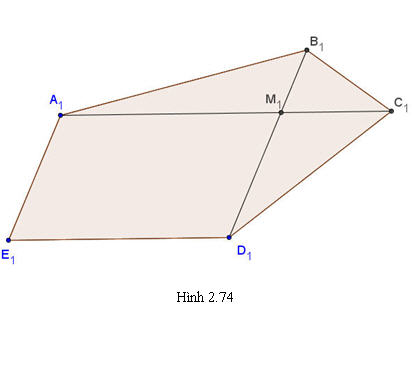
Tải trực tiếp tệp hình học động:L11_Ch2_h2.74.ggb
Xem trực tiếp hình vẽ động trên màn hình.
Mặt khác, vì tứ giác MADE là hình thoi nên AM = AE = BC, do đó: 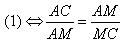
Đặt AM = a, MC = x, ta có: 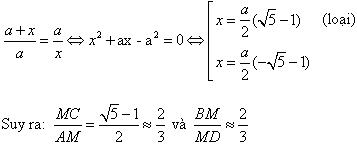
Các tỉ số này giữ nguyên trên hình biểu diễn . Để xác định hình biểu diễn , ta vẽ một hình bình hành A1M1D1E1 bất kì làm hình biểu diễn của hình thoi MADE (h.2.74). Sau đó kéo dài cạnh A1M1 một đoạn M1C1 = 2/3 M1A1 và kéo dài cạnh D1M1 thêm một đoạn M1B1 = 2/3 M1D1. Nối các điểm A1, B1, C1, D1, E1 theo thứ tự đó, ta được hình biểu diễn của một ngũ giác đều.
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng và đường thẳng
và đường thẳng 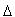 cắt
cắt 
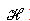 là một hình nào đó thì tập hợp
là một hình nào đó thì tập hợp 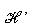 các hình chiếu M’ của tất cả những điểm M thuộc
các hình chiếu M’ của tất cả những điểm M thuộc 









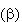 song song với nhau. Đường thẳng a cắt
song song với nhau. Đường thẳng a cắt