Trong chương này, chúng ta sẽ nghiên cứu về vectơ trong không gian, đồng thời dựa vào các kiến thức có liên quan đến tập hợp các vectơ trong không gian để xây dựng quan hệ vuông góc của đường thẳng, mặt phẳng trong không gian. Ở lớp 10 chúng ta đã được học về vectơ trong mặt phẳng. Những kiến thức có liên quan đến vectơ đã giúp chúng ta làm quen với phương pháp dùng vectơ và dùng tọa độ để nghiên cứu hình học phẳng. Chúng ta biết rằng tập hợp các vectơ nằm trong mặt phẳng nào đó là một bộ phận của tập hợp các vectơ trong không gian. Do đó định nghĩa vectơ trong không gian cùng với một số nội dung có liên quan đến vectơ như độ dài của vectơ, sự cùng phương, cùng hướng của hai vectơ, giá của vectơ, sự bằng nhau của hai vectơ và các quy tắc thực hiện các phép toán về vectơ được xây dựng và xác định hoàn toàn tương tự như trong mặt phẳng. Tất nhiên trong không gian, chúng ta sẽ gặp những vấn đề mới về vectơ như việc xét sự đồng phẳng hoặc không đồng phẳng của ba vectơ hoặc việc phân tích một vectơ theo ba vectơ không đồng phẳng. Những nội dung này sẽ được xét đến trong các phần tiếp theo sau đây.
I. Định nghĩa và các phép toán về vectơ trong không gian
Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A, điểm cuối là B ta có một vectơ, được kí hiệu là 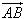 . . 1. Định nghĩa Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu 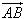 chỉ vectơ có điểm đầu A, điểm cuối B. Vectơ còn được kí hiệu là chỉ vectơ có điểm đầu A, điểm cuối B. Vectơ còn được kí hiệu là 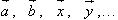 Các khái niệm có liên quan đến vectơ như giá của vectơ, độ dài của vectơ, sự cùng phương, cùng hướng của hai vectơ, vectơ- không, sự bằng nhau của hai vectơ,… được định nghĩa tương tự như trong mặt phẳng. Các khái niệm có liên quan đến vectơ như giá của vectơ, độ dài của vectơ, sự cùng phương, cùng hướng của hai vectơ, vectơ- không, sự bằng nhau của hai vectơ,… được định nghĩa tương tự như trong mặt phẳng. ?1. hình tứ diện ABCD. Hãy chỉ ra các vectơ có điểm đầu là A và điểm cuối là các đỉnh còn lại của hình tứ diện. Các vectơ đó có cùng nằm trong một mặt phẳng không? ?2. Cho hình hộp ABCD.A’B’C’D’. Hãy kể tên các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vectơ 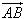 . . 2. Phép cộng và phép trừ vectơ trong không gian Phép cộng và phép trừ hai vectơ trong không gian được định nghĩa tương tự như phép cộng và phép trừ hai vectơ trong mặt phẳng. Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng. Khi thực hiện phép cộng vectơ trong không gian ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vectơ trong hình học phẳng. Ví dụ 1. Cho tứ diện ABCD. Chứng minh: 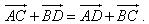 Giải: Theo quy tắc ba điểm ta có:
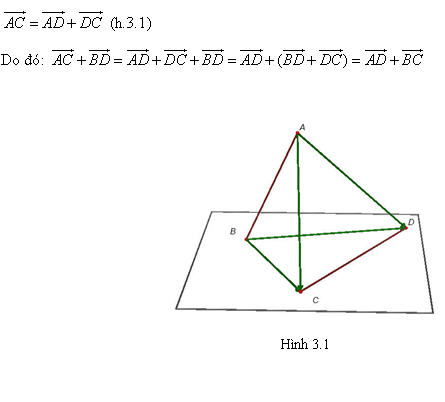
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.1.cg3
Xem trực tiếp hình vẽ động trên màn hình.
?3. Cho hình hộp ABCD.EFGH. Hãy thực hiện các phép toán sau đây (h.3.2):
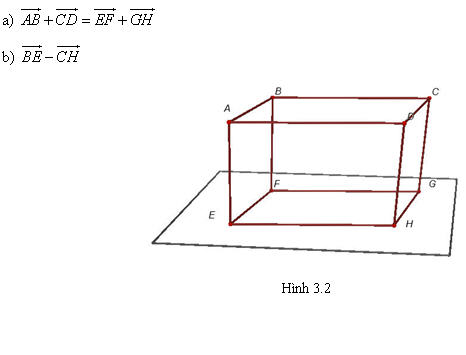
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.2.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Quy tắc hình hộp
Cho hình hộp ABCD.A’B’C’D’ có ba cạnh xuất phát từ đỉnh A là AB, AD, AA’ và có đường chéo là AC’. Khi đó ta có quy tắc hình hộp là: 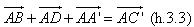
Quy tắc này được suy ra từ quy tắc hình bình hành trong hình học phẳng.
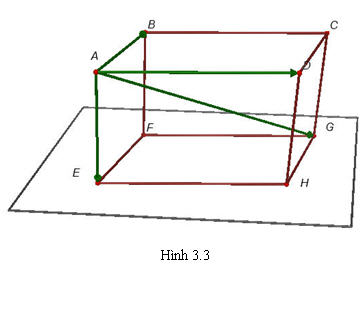
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.3.cg3
Xem trực tiếp hình vẽ động trên màn hình.
3. Phép nhân vectơ với một số
Trong không gian, tích của vectơ 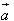 với một số k với một số k 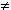 0 là vectơ 0 là vectơ 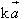 được định nghĩa tương tự như trong mặt phẳng và có các tính chất giống như các tính chất đã được xét trong mặt phẳng. được định nghĩa tương tự như trong mặt phẳng và có các tính chất giống như các tính chất đã được xét trong mặt phẳng. Ví dụ 2. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm của tam giác BCD. Chứng minh rằng: 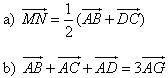
Giải:
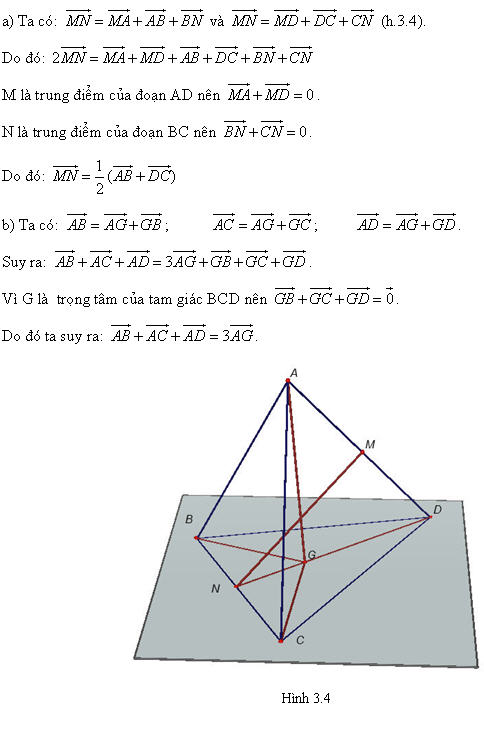
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.4.cg3
Xem trực tiếp hình vẽ động trên màn hình.
?4. Trong không gian cho hai vectơ  và và  đều khác vectơ-không. Hãy xác định các vectơ: đều khác vectơ-không. Hãy xác định các vectơ: 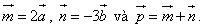
II. Điều kiện đồng phẳng của ba vectơ
1. Khái niệm về sự đồng phẳng của ba vectơ trong không gian Trong không gian cho ba vectơ 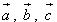 đều khác vectơ-không. Nếu từ một điểm O bất kì ta vẽ đều khác vectơ-không. Nếu từ một điểm O bất kì ta vẽ 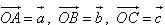 thì có thể xảy ra hai trường hợp: thì có thể xảy ra hai trường hợp: + Trường hợp các đường thẳng OA, OB, OC không cùng nằm trong một mặt phẳng, khi đó ta nói rằng ba vectơ 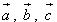 không đồng phẳng (h.3.5a). không đồng phẳng (h.3.5a). + Trường hợp các đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng thì ta nói ba vectơ 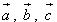 đồng phẳng (h.3.5b). đồng phẳng (h.3.5b). Trong trường hợp này giá của các vectơ 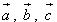 luôn luôn song song với một mặt phẳng. luôn luôn song song với một mặt phẳng.
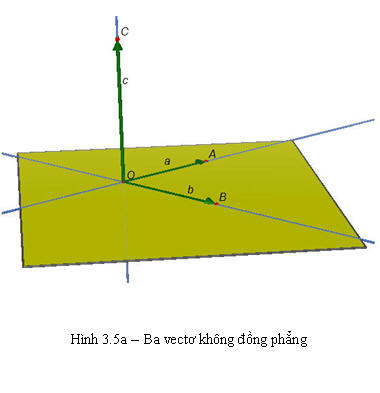
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.5a.cg3
Xem trực tiếp hình vẽ động trên màn hình.
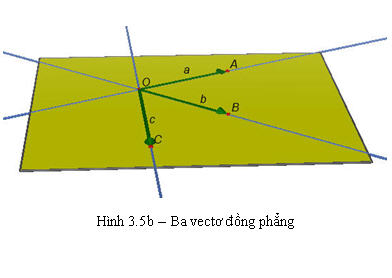
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.5b.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Chú ý: Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vectơ nói trên phụ thuộc vào việc chọn điểm O. Từ đó ta có định nghĩa sau đây: 2. Định nghĩa Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng. (h.3.6).
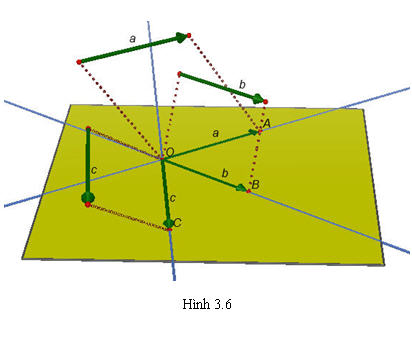
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.6.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Ví dụ 3. Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng ba vectơ  đồng phẳng. đồng phẳng. Giải: Gọi P, Q lần lượt là trung điểm của AC và BD (h.3.7). Ta có PN song song với MQ và PM = MQ = 1/2 AD. Vậy tứ giác MNPQ là hình bình hành. Mặt phẳng (MPNQ) chứa đường thẳng MN và song song với các đường thẳng AD và BC. Ta suy ta ba đường thẳng MN, AD, BC cùng song song với một mặt phẳng. Do đó ba vectơ 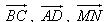 đồng phẳng. đồng phẳng.
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.7.cg3
Xem trực tiếp hình vẽ động trên màn hình.
?5. Cho hình hộp ABCD.EFGH. Gọi I và K lần lượt là trung điểm của các cạnh AB và BC. Chứng minh rằng các đường thẳng IK và ED song song với mặt phẳng (AFC). Từ đó suy ra ba vectơ 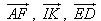 đồng phẳng. đồng phẳng. 3. Điều kiện để ba vectơ đồng phẳng. Từ định nghĩa ba vectơ đồng phẳng và từ định lí về sự phân thích (hay biểu thị) một vectơ theo hai vectơ không cùng phương trong hình học phẳng chúng ta có thể chứng minh được định lí sau đây: Định lí 1 Trong không gian cho hai vectơ 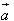 , , 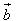 không cùng phương và vectơ không cùng phương và vectơ 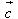 . Khi đó ba vectơ . Khi đó ba vectơ 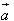 , , 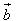 , , 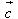 đồng phẳng khi và chỉ khi có các cặp số m, n sao cho đồng phẳng khi và chỉ khi có các cặp số m, n sao cho 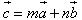 . Ngoài ra cặp số m, n là duy nhất. . Ngoài ra cặp số m, n là duy nhất. ?6. Cho hai vectơ 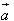 , , 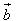 đều khác vecơ đều khác vecơ 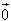 . Hãy xác định vectơ . Hãy xác định vectơ 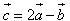 và giải thích tại sao ba vectơ và giải thích tại sao ba vectơ 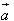 , , 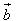 , , 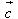 đồng phẳng. đồng phẳng. ?7. Cho ba vectơ 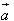 , , 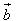 , , 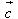 trong không gian. Chứng minh rằng nếu trong không gian. Chứng minh rằng nếu 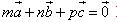 và một trong ba số m, n, p khác không thì ba vectơ và một trong ba số m, n, p khác không thì ba vectơ 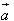 , , 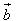 , , 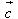 đồng phẳng. đồng phẳng. Ví dụ 4. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Trên các cạnh AD và BC lần lượt lấy các điểm P, Q sao cho: 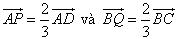
Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một mặt phẳng. Giải:
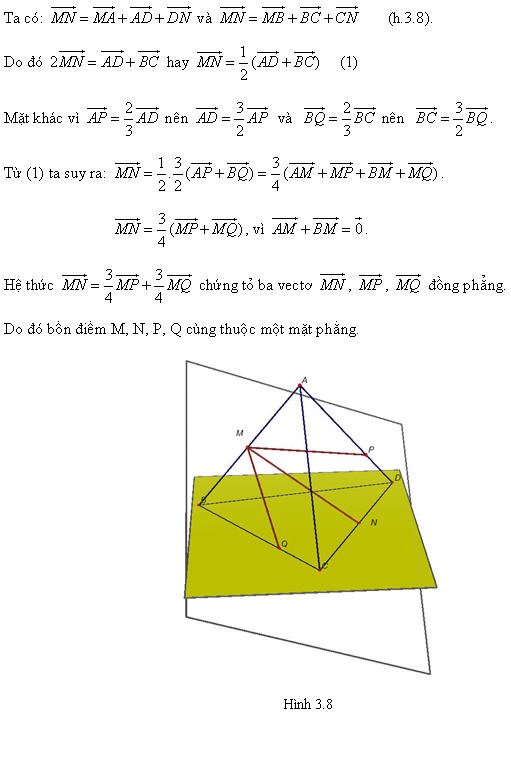
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.8.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Định lí 1 cho ta phương pháp chứng minh sự đồng phẳng của ba vectơ thông qua việc biểu thị một vectơ theo hai vectơ không cùng phương. Về việc biểu thị một vectơ bất kì theo ba vectơ không đồng phẳng trong không gian, người ta chứng minh được định lí sau đây. Định lí 2 Trong không gian cho ba vectơ không đồng phẳng 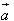 , , 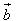 , , 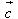 . Khi đó với mọi vectơ . Khi đó với mọi vectơ 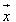 ta đều tìm được một bộ ba số m,n,p sao cho ta đều tìm được một bộ ba số m,n,p sao cho 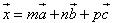 . Ngoài ra bộ ba số m, n, p là duy nhất (h.3.9). . Ngoài ra bộ ba số m, n, p là duy nhất (h.3.9).
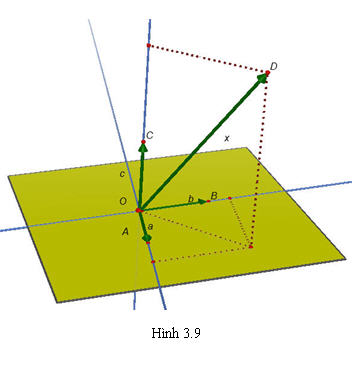
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.9.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Ví dụ 5. Cho hình hộp ABCD. EFGH có 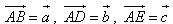 . Gọi I là trung điểm của đoạn BG. Hãy biểu thị vectơ . Gọi I là trung điểm của đoạn BG. Hãy biểu thị vectơ 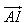 qua ba vectơ qua ba vectơ 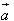 , , 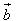 , , 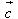 . . Giải: Vì I là trung điểm của đoạn BG nên ta có:
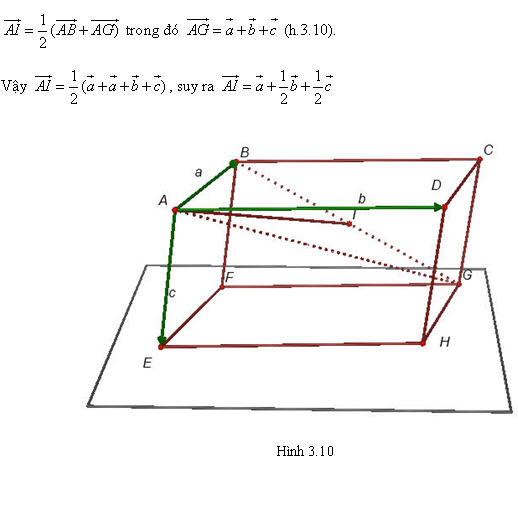
Tải trực tiếp tệp hình học động ( Nhấn chuột phải vào liên kết rồi chọn Save As):L11_Ch3_h3.10.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Bài tập
1. Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Mặt phẳng (P) cắt các cạnh bên AA’, BB’, CC’, DD’ lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ: a) Cùng phương với 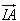 b) Cùng hướng với 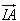 c) Ngược hướng với 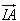 . . 2. Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng: 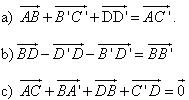
3. Cho hình bình hành ABCD. Gọi S là một điểm nằm ngoài mặt phẳng chứa hình bình hành. Chứng minh rằng: 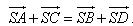
4. Cho hình tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng: 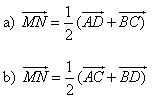
5. Cho hình tứ diện ABCD. Hãy xác định hai điểm E, F sao cho: 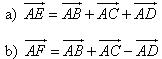
6. Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng: 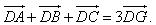
7. Gọi M và N lần lượt là trung điểm của các cạnh AC và BD cứ tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh rằng: 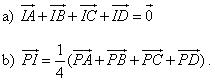
8. Cho hình lăng trụ tam giác ABC.A’B’C’ có: 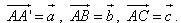
Hãy phân tích hay biểu thị các vectơ 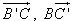 qua các vectơ qua các vectơ 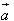 , , 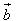 , , 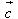 . . 9. Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho 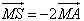 và trên đoạn BC lấy điểm N sao cho và trên đoạn BC lấy điểm N sao cho 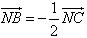 . Chứng minh rằng ba vectơ . Chứng minh rằng ba vectơ 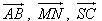 đồng phẳng. đồng phẳng. 10. Cho hình hộp ABCD.EFGH. Gọi K là giao điểm của AH và DE, I là giao điểm của BH và DF. Chứng minh ba vectơ 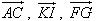 đồng phẳng. đồng phẳng.
schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng .
.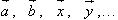 Các khái niệm có liên quan đến vectơ như giá của vectơ, độ dài của vectơ, sự cùng phương, cùng hướng của hai vectơ, vectơ- không, sự bằng nhau của hai vectơ,… được định nghĩa tương tự như trong mặt phẳng.
Các khái niệm có liên quan đến vectơ như giá của vectơ, độ dài của vectơ, sự cùng phương, cùng hướng của hai vectơ, vectơ- không, sự bằng nhau của hai vectơ,… được định nghĩa tương tự như trong mặt phẳng.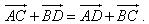


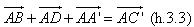

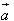 với một số k
với một số k 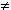 0 là vectơ
0 là vectơ 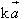 được định nghĩa tương tự như trong mặt phẳng và có các tính chất giống như các tính chất đã được xét trong mặt phẳng.
được định nghĩa tương tự như trong mặt phẳng và có các tính chất giống như các tính chất đã được xét trong mặt phẳng.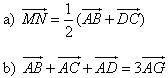

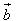 đều khác vectơ-không. Hãy xác định các vectơ:
đều khác vectơ-không. Hãy xác định các vectơ: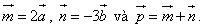
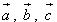 đều khác vectơ-không. Nếu từ một điểm O bất kì ta vẽ
đều khác vectơ-không. Nếu từ một điểm O bất kì ta vẽ 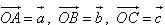 thì có thể xảy ra hai trường hợp:
thì có thể xảy ra hai trường hợp:


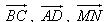 đồng phẳng.
đồng phẳng.
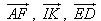 đồng phẳng.
đồng phẳng.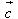 . Khi đó ba vectơ
. Khi đó ba vectơ 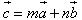 . Ngoài ra cặp số m, n là duy nhất.
. Ngoài ra cặp số m, n là duy nhất. . Hãy xác định vectơ
. Hãy xác định vectơ 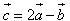 và giải thích tại sao ba vectơ
và giải thích tại sao ba vectơ 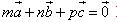 và một trong ba số m, n, p khác không thì ba vectơ
và một trong ba số m, n, p khác không thì ba vectơ 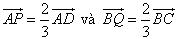

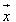 ta đều tìm được một bộ ba số m,n,p sao cho
ta đều tìm được một bộ ba số m,n,p sao cho 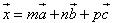 . Ngoài ra bộ ba số m, n, p là duy nhất (h.3.9).
. Ngoài ra bộ ba số m, n, p là duy nhất (h.3.9).
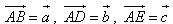 . Gọi I là trung điểm của đoạn BG. Hãy biểu thị vectơ
. Gọi I là trung điểm của đoạn BG. Hãy biểu thị vectơ  qua ba vectơ
qua ba vectơ 
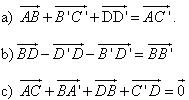
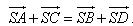
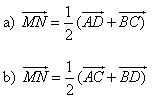
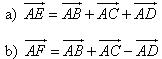
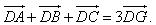
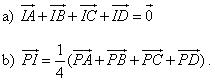
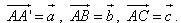
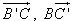 qua các vectơ
qua các vectơ 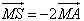 và trên đoạn BC lấy điểm N sao cho
và trên đoạn BC lấy điểm N sao cho 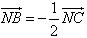 . Chứng minh rằng ba vectơ
. Chứng minh rằng ba vectơ 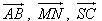 đồng phẳng.
đồng phẳng.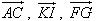 đồng phẳng.
đồng phẳng.

