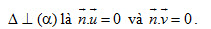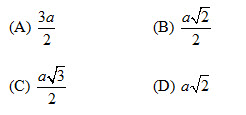3. Trong không gian hai đường thẳng không cắt nhau có thể vuông góc với nhau.không? Giả sử hai đường thẳng a và b lần lượt có vectơ chỉ phương 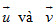 khi nào ta có thể kết luận a và b vuông góc với nhau khi nào ta có thể kết luận a và b vuông góc với nhau
4. Muốn chứng minh đường thẳng a vuông góc với mặt phẳng 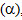 có cần chứng minh a vuông góc với mọi đường thẳng của có cần chứng minh a vuông góc với mọi đường thẳng của 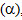 hay không? hay không?
5. Hãy nhắc lại nội dung định lí ba đường vuông góc.
6. Hãy nhắc lại định nghĩa
a) Góc giữa đường thẳng và mặt phẳng
b) Góc giữa hai mặt phẳng.
7. Muốn chứng minh mặt phẳng 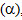 vuông góc với mặt phẳng vuông góc với mặt phẳng 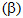 thì phải chứng minh như thế nào? thì phải chứng minh như thế nào?
8. Hãy nếu cách tính khoảng cách:
a) Từ một điểm đến một đường thẳng;
b) Từ đường thẳng a đến mặt phẳng 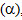 song song với a; song song với a;
c) Giữa hai mặt phẳng song song.
9. Cho a và b là hai đường thẳng chéo nhau. Có thể tính khoảng cách giữa hai đường thẳng chéo nhau này bằng những cách nào?
10. Chứng minh rằng tập hợp các điểm cách đều ba đỉnh của tam giác ABC là đường thẳng vuông góc với mặt phẳng (ABC) và đi qua tâm của đường tròn ngoại tiếp tam giác ABC. BÀI TẬP ÔN TẬP CHƯƠNG III 1. Trong các mệnh đề sau, mệnh đề nào là đúng?
a) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song;
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song;
c) Mặt phẳng 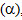 vuông góc với đường thẳng b mà b vuông góc với đường thẳng a, thì a song song với vuông góc với đường thẳng b mà b vuông góc với đường thẳng a, thì a song song với 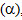 . .
d) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song;
e) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song.
2. Trong các điều khẳng định sau đây, điều nào đúng?
a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại;
b) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác;
c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác.
d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
3. Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA bằng a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng 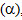 đi qua A và vuông góc với cạnh SC lần lượt cắt SB, DC, SD tại B’, C’, D’. Chứng minh B’D’ song song với BD và AB’ vuông góc với SB. đi qua A và vuông góc với cạnh SC lần lượt cắt SB, DC, SD tại B’, C’, D’. Chứng minh B’D’ song song với BD và AB’ vuông góc với SB.
4. Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có góc 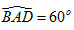 . Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và . Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và 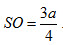 . Gọi E là trung điểm của đoạn BC, F là trung điểm của đoạn BE. . Gọi E là trung điểm của đoạn BC, F là trung điểm của đoạn BE.
a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).
b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).
5. Tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau.
Tam giác ABC vuông tại A có AB = a, AC = b. Tam giác ADC vuông tại D có CD = a.
a) Chứng minh các tam giác BAD và BDC là những tam giác vuông.
b) Gọi I và K lần lượt là trung điểm của AD và BC. Chứng minh IK là đường vuông góc chung của hai đường thẳng AD và BC.
6. Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
a) Xác định BC’ vuông góc với mặt phẳng (A’B’CD).
b) Xác định và tính độ dài đoạn vuông góc chung của AB’ và BC’.
7. Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a có góc 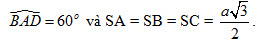
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC
d) Gọi 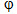 kà góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tan kà góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tan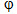 . . CÂU HỎI TRẮC NGHIỆM CHƯƠNG III 1. Trong các mệnh đề sau, mệnh đề nào là đúng? 
2. Tìm mệnh đề sai trong các mệnh đề sau đây:
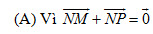
nên N là trung điểm của đoạn MP.
(B) Vì I là trung điểm của đoạn AB nên từ một điểm O bất kì ta có:
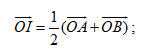
(C) Từ hệ thức 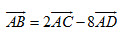 ta suy ra ba vectơ ta suy ra ba vectơ 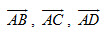 đồng phẳng; đồng phẳng;
(D) Vì 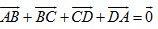 nên bốn điểm A, B,C,D cùng thuộc một mặt phẳng. nên bốn điểm A, B,C,D cùng thuộc một mặt phẳng.
3. Trong các kết quả sau đây, kết quả nào đúng?
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Ta có 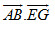 bằng bằng
4. Trong các mệnh đề sau đây, mệnh đề nào là đúng?
(A) Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a vuông góc với c;
(B) Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng c thì a vuông góc với c.
(C) Cho ba đường thẳng a, b, c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d vuông góc với a thì d song song với b hoặc c;
(D) Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong mặt phẳng (a,b).
5. Trong các mệnh đề sau đây, hãy tìm mệnh đề đúng.
(A) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
(B) Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt phẳng kia.
(C) Hai mặt phẳng 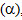 và và 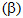 vuông góc với nhau và cắt nhau theo giao tuyến d. Với mỗi điểm A thuộc () và mỗi điểm B thuộc vuông góc với nhau và cắt nhau theo giao tuyến d. Với mỗi điểm A thuộc () và mỗi điểm B thuộc 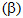 thì ta có đường thẳng AB vuông góc với d. thì ta có đường thẳng AB vuông góc với d.
(D) Nếu hai mặt phẳng 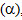 và và 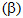 đều vuông góc với mặt phẳng () thì giao tuyến d của đều vuông góc với mặt phẳng () thì giao tuyến d của 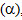 và và 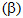 nếu có sẽ vuông góc với (). nếu có sẽ vuông góc với ().
6. Tìm mệnh đề sai trong các mệnh đề sau:
(A) Hai đường thẳng a và b trong không gian có các vectơ chỉ phương lần lượt là 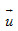 và và 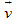 . Điều kiện cần và đủ để a và b chéo nhau là a và b không có điểm chung và hai vectơ . Điều kiện cần và đủ để a và b chéo nhau là a và b không có điểm chung và hai vectơ 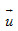 , , 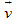 không cùng phương; không cùng phương;
(B) Cho a, b là hai đường thẳng chéo nhau và vuông góc với nhau. Đường vuông góc chung của a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia;
(C) Không thể có một hình chóp tứ giác S.ABCD nào có hai mặt bên (SAB) và (SCD) cùng vuông góc với mặt phẳng đáy;
(D) Cho 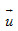 , , 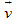 là hai vectơ chỉ phương của hai đường thẳng cắt nhau nằm trong mặt phẳng là hai vectơ chỉ phương của hai đường thẳng cắt nhau nằm trong mặt phẳng 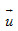 và và 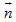 là vectơ chỉ phương của đường thẳng . Điều kiện cần và đủ để là vectơ chỉ phương của đường thẳng . Điều kiện cần và đủ để 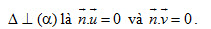
7. Trong các mệnh đề sau đây, mệnh đề nào là đúng?
(A) Một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng.
(B) Một đường thẳng cắt hai đường thẳng cắt nhau cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng.
(C) Ba đường thẳng cắt nhau từng đôi một thì cùng nằm trong một mặt phẳng.
(D) Ba đường thẳng cắt nhau từng đôi một và không nằm trong một mặt phẳng thì đồng quy.
8. Trong các mệnh đề sau, mệnh đề nào là đúng?
(A) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
(B) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
(C) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
(D) Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
9. Trong các mệnh đề sau, mệnh đề nào là đúng?
(A) Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
(B) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
(C) Hai đường thẳng phân biệt cũng vuông góc với một đường thẳng thì vuông góc với nhau.
(D) Một mặt phẳng 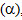 và một đường thẳng a không thuộc và một đường thẳng a không thuộc 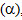 cũng vuông góc với đường thẳng b thì cũng vuông góc với đường thẳng b thì 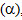 song song với a. song song với a.
10. Tìm mệnh đề đúng trong các mệnh đề sau:
(A) Đoạn vuông góc chung của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy và ngược lại.
(B) Qua một điểm cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
(C) Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với một đường thẳng cho trước.
(D) Cho ba đường thẳng a, b, c chéo nhau từng đôi một. Khi đó ba đường thẳng này sẽ nằm trong ba mặt phẳng song song với nhau từng đôi một.
11. Khoảng cách giữa hai cạnh đối diện của một tứ diện đều có cạnh a bằng kết quả nào trong các kết quả sau đây? 
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.  đều khác vectơ-không. Khi nào ba vectơ đó đồng phẳng.
đều khác vectơ-không. Khi nào ba vectơ đó đồng phẳng. 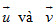 khi nào ta có thể kết luận a và b vuông góc với nhau
khi nào ta có thể kết luận a và b vuông góc với nhau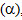 có cần chứng minh a vuông góc với mọi đường thẳng của
có cần chứng minh a vuông góc với mọi đường thẳng của 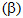 thì phải chứng minh như thế nào?
thì phải chứng minh như thế nào? 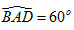 . Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và
. Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và 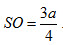 . Gọi E là trung điểm của đoạn BC, F là trung điểm của đoạn BE.
. Gọi E là trung điểm của đoạn BC, F là trung điểm của đoạn BE. 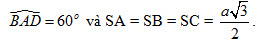
 kà góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tan
kà góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tan
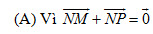
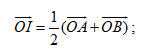
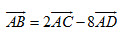 ta suy ra ba vectơ
ta suy ra ba vectơ 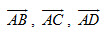 đồng phẳng;
đồng phẳng; 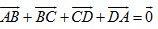 nên bốn điểm A, B,C,D cùng thuộc một mặt phẳng.
nên bốn điểm A, B,C,D cùng thuộc một mặt phẳng. 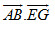 bằng
bằng
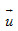 và
và 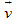 . Điều kiện cần và đủ để a và b chéo nhau là a và b không có điểm chung và hai vectơ
. Điều kiện cần và đủ để a và b chéo nhau là a và b không có điểm chung và hai vectơ 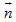 là vectơ chỉ phương của đường thẳng . Điều kiện cần và đủ để
là vectơ chỉ phương của đường thẳng . Điều kiện cần và đủ để