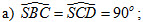c) Phép đối xứng qua tâm I(2;1);
d) Phép quay tâm O góc 90o;
e) Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép vị tự tâm O tỉ số k = -2.
2. Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi G và H tương ứng là trọng tâm và trực tâm của tam giác, các điểm A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB.
a) Tìm phép vị tự F biến A, B, C tương ứng thành A’, B’, C’.
b) Chứng minh rằng O, G, H thẳng hàng.
c) Tìm ảnh của O qua phép vị tự F.
d) Gọi A’’, B’’, C’’ lần lượt là trung điểm của các đoạn thẳng AH, BH, CH; A1, B1,
C1 theo thứ tự là giao điểm thứ hai của các tia AH, BH, CH với đường tròn (O); A’1, B’1, C’1 tương ứng là chân các đường cao đi qua A, B, C. Tìm ảnh của A, B, C, A1, B1, C1 qua phép vị tự tâm H tỉ số 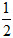 . .
e) Chứng minh chín điểm A’, B’, C’, A’’, B’’, C’’, A’1, B’1, C’1 cùng thuộc một đường tròn (đường tròn này gọi là đường tròn Ơ-le của tam giác ABC).
3. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh bên của hình thang ABCD và G là trọng tâm của tam giác ECD.
a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.
b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
c) Lấy một điểm K trên đoạn SE và gọi C’ = SC ∩ KB, D’ = SD ∩ KA. Chứng minh rằng giao điểm của AC’ và BD’ thuộc đường thẳng d nói trên.
4. Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có E, F, M và N lần lượt là trung điểm của AC, BD, AC’ và BD’ . Chứng minh MN = EF.
5. Cho hình lập phương ABCD.A’B’C’D’ có E và F lần lượt là trung điểm của các cạnh AB và DD’. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC’) và (EFK) với K là trung điểm của cạnh B’C’.
6. Cho hình lập phương ABCD.A’B’C’D’ có các cạnh bằng a.
a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau BD’ và B’C.
b) Tính khoảng cách của hai đường thẳng BD’ và B’C.
7. Cho hình thang ABCD vuông tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng:
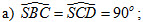
b) AD’, AC’ và AB cùng nằm trên một mặt phẳng.
c) Chứng minh rằng đường thẳng C’D’ luôn luôn đi qua một điểm cố định khi S di động trên tia Ax.
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng ;
;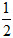 .
.