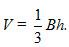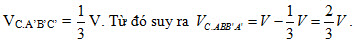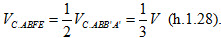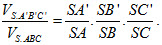Đối với những vật thể lỏng, như khối nước trong một cái bể chứa, người ta có thể dùng những cái thùng có kích thước nhỏ hơn để đong. Đối với những vật rắn có kích thước nhỏ người ta có thể thả chúng vào một cái thùng đổ đầy nước rồi đo lượng nước trào ra... Tuy nhiên trong thực tế có nhiều vật thể không thể đo được bằng những cách trên. Chẳng hạn để đo thể tích của kim tự tháp Ai Cập ta không thể nhúng nó vào nước hay chia nhỏ nó ra được. Vì vậy người ta tìm cách thiết lập những công thức tính thể tích của một số khối đa diện đơn giản khi biết kích thước của chúng, rồi từ đó tìm cách tính thể tích của các khối đa diện phức tạp hơn.
I. KHÁI NIỆM VỀ THỂ TÍCH KHỐI ĐA DIỆN
Người ta chứng minh được rằng : có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất V(H) thoả mãn các tính chất sau:
a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.
b) Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2)
c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì: V(H) = V(H1) + V(H2)
Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Số đó cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).
Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.
Bây giờ ta sẽ xét thể tích của khối hộp chữ nhật có ba kích thước là a, b, c.
Ví dụ. Tính thể tích của khối hộp chữ nhật có ba kích thước là những số nguyên dương.
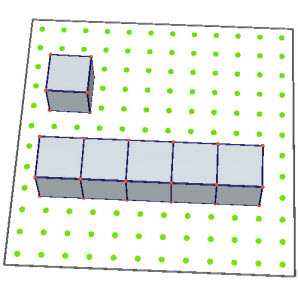
Hình 1.25
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch1_h1.25.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
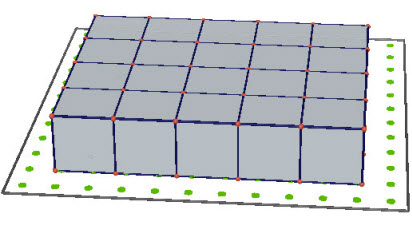
Hình 1.25a
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch1_h1.25a.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
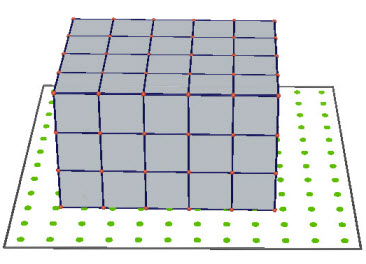
Hình 1.25c
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch1_h1.25c.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Gọi (H0) là khối lập phương đơn vị.
- Gọi (H1) là khối hộp chữ nhật có ba kích thước a = 5, b = 1, c= 1.
1 Có thể chia (H1) thành bao nhiêu khối lập phương bằng (H0) ?
Khi đó ta có V(H1) = 5.V(H0) = 5
- Gọi (H2) là khối hộp chữ nhật có ba kích thước a = 5, b = 4, c = 1.
2 Có thể chia (H2) thành bao nhiêu khối hộp chữ nhật bằng (H1) ?
Khi đó ta có V(H2) = 4.V(H1) = 4.5 = 20
- Gọi (H) là khối hộp chữ nhật có ba kích thước a = 5, b = 4, c = 3.
3 Có thể chia (H) thành bao nhiêu khối hộp chữ nhật bằng (H2) ?
Khi đó ta có V(H) = 3.V(H2) = 3.4.5 = 60 (h.1.25).
Lập luận tương tự trên, ta suy ra: thể tích của khối hộp chữ nhật (H) có ba kích thước là những số nguyên dương a, b, c là V(H) = abc.
Người ta chứng minh được rằng công thức trên cũng đúng đối với hình hộp chữ nhật có ba kích thước là những số dương. Ta có định lí sau:
Định lí
Thể tích của một khối hộp chữ nhật bằng tích ba kích thước của nó.
II. THỂ TÍCH KHỐI LĂNG TRỤ
Nếu ta xem khối hộp chữ nhật ABCD.A’B’C’D’ như là khối lăng trụ có đáy là hình chữ nhật A’B’C’D’ và đường cao AA’ thì từ định lí trên suy ra thể tích của nó bằng diện tích đáy nhân với chiều cao. Ta có thể chứng minh được rằng điều đó cũng đúng với một khối lăng trụ bất kì (h.1.26).
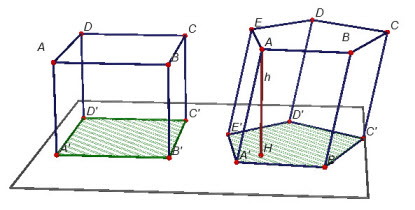
Hình 1.26
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch1_h1.26.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Định lí
Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là
V = Bh.
III-THỂ TÍCH KHỐI CHÓP
Đối với khối chóp, người ta chứng minh được định lí sau:
Định lí
Thể tích của khối chóp có diện tích đáy B và chiều cao h là
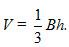
Ta cũng gọi thể tích các khối đa diện, khối lăng trụ, khối chóp đã nói ở trên lần lượt là thể tích các hình đa diện, hình lăng trụ, hình chóp xác định chúng.
4 Kim tự tháp ở Ai Cập (h.1.27) được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147m, cạnh đáy dài 230m. Hãy tính thể tích của nó.

Hình 1.27
Tải trực tiếp tệp hình học động:L12cb_Ch1_h1.27.ggb Xem trực tiếp hình vẽ động trên màn hình.
Ví dụ
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi E và F lần lượt là trung điểm của các cạnh AA’ và BB’. Đường thẳng CE cắt đường thẳng C’A’ tại E’. Đường thẳng CF cắt đường thẳng C’B’ tại F’. Gọi V là thể tích khối lăng trụ ABC.A’B’C’.
a) Tính thể tích khối chóp C.ABFE theo V.
b) Gọi khối đa diện (H) là phần còn lại của khối lăng trụ ABC.A’B’C’ sau khi cắt bỏ đi khối chóp C.ABFE. Tính tỉ số thể tích của (H) và của khối chóp C.C’E’F’.
Giải
a) Hình chóp C.A’B’C’ và hình lăng trụ ABC.A’B’C’ có đáy và đường cao bằng nhau nên
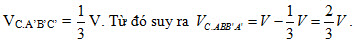
Do EF là đường trung bình của hình bình hành ABB’A’ nên diện tích ABFE bằng nửa diện tích ABB’A’. Do đó
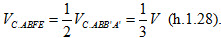
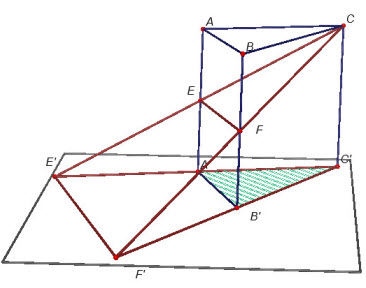
Hình 1.28
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch1_h1.28.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )

BÀI TẬP
1. Tính thể tích khối tứ diện đều cạnh a.
2. Tính thể tích khối bát diện đều cạnh a.
3. Cho hình hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
4. Cho hình chóp S.ABC. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A’, B’, C’ khác với S. Chứng minh rằng:
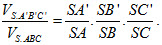
5. Cho tam giác ABC vuông cân ở A và AB = a. Trên đường thẳng qua C và vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với BD, cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a.
6. Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài a trượt trên d, đoạn thẳng CD có độ dài b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng