Nhận xét trên là cơ sở cho định nghĩa sau đây:
2. Hai mặt phẳng vuông góc.
Định nghĩa: Hai mặt phẳng gọi là vuông góc với nhau nếu trong một hai mặt phẳng đó chứa một đường thẳng vuông góc với mặt phẳng kia.
Để kí hiệu hai mặt phẳng (P) và (Q) vuông góc với nhau ta viết.
(P) ⊥ (Q) hay
(Q) ⊥ (P)
Hình 67. Định nghĩa hai mặt phẳng vuông góc.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Điểm A chuyển động tự do trong không gian. Đường thẳng a luôn đi qua A và vuông góc với mặt phẳng Q. Mặt phẳng P đi qua a và một điểm trên Q. Đường thẳng B đi qua điểm B và vuông góc với P. Dịch chuyển A, B và điểm (màu đỏ) trên C để quan sát hình vẽ .
3. Các tính chất.
Định lý 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyết thì vuông góc với mặt phẳng kia.
Chứng minh: Giả sử hai mặt phẳng (P) và (Q) vuông góc. Gọi c là giao tuyến của (P) và (Q). Gọi a là đường thẳng chứa trong mp(P) và a ⊥c ta chứng minh a⊥(Q).
Hình 68. Minh họa cho định lý 1.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Mặt phẳng nằm ngang Q được xác định bởi 3 điểm X, Y, Z chuyển động tự do trong không gian. Mặt phẳng P luôn đi qua 2 điểm M, N chuyển động tự do trong không gian và vuông góc với Q. Điểm A chuyển động tự do trong P và đường thẳng a đi qua A và vuông góc với Q.
Thật vậy do (Q) ⊥ (P) nên trong (Q) có đường thẳng b ⊥ (P) suy ra b ⊥ a.
a ⊥ c và a ⊥ b ⇒ a ⊥ (Q)
Định lý 2: Nếu hai mặt p hẳng (P) và (Q) vuông góc với nhau và A là điểm nằm trên (P) thì đường thẳng a đi qua A và vuông góc với (Q) sẽ nằm trong (P).
Chứng minh: Ta kẻ đường thẳng a' nằm trong mp(P) đi qua A và vuông góc với giao tuyến c của (P) và (Q)
Hình 69. Minh họa cho định lý 2.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Mặt phẳng nằm ngang Q được xác định bởi 3 điểm X, Y, Z chuyển động tự do trong không gian. Mặt phẳng P luôn đi qua 2 điểm M, N chuyển động tự do trong không gian và vuông góc với Q.
Điểm A chuyển động tự do trong không gian. Đường thẳng a luôn đi qua A và vuông góc với Q.
Dịch chuyển A theo phương nằm ngang cho đến khi A đi qua P và quan sát a để minh họa cho tính đúng đắn của định lý.
Theo định lý 1 ta có a'⊥(Q) và do chỉ có một đường thẳng duy nhất qua A và vuông góc với (Q) nên a trùng với a' vậy a phải nằm trong (P).
Định lý 3: Hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của hai mặt phẳng đó cùng vuông góc với mặt phẳng thứ ba.
Chứng minh: Giả sử (P) ⊥ (R), (Q) ⊥ (R) và O là điểm chung của (P) và (Q)
Hình 70. Minh họa cho định lý 3.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Các mặt phẳng P, Q được xác định bởi 2 điểm chuyển động tự do trên mặt phẳng nằm ngang (màu xanh) và luôn vuông góc với mặt phẳng nằm ngang. Dịch chuyển các điểm này để quan sát sự thay đổi của P, Q. Khi hai mặt phẳng này cắt nhau, giao của chúng luôn vuông góc với mặt phẳng nằm ngang.
Gọi a là đường thẳng đi qua O và vuông góc với (R). Theo định lí 2 ta có a ⊂(P). và a ⊂ (Q) suy ra a = (P) ∩ (Q).
Vậy giao tuyến a của (P) và (Q) vuông góc với mp(R).
Định lý 4: Qua một đường thẳng a không vuông góc với mp(P) có một và chỉ mp(Q) vuông góc với mp(P).
Chứng minh: Từ điểm O nằm trên a ta kẻ đường thẳng b ⊥ mp(P)
Hình 71. Minh họa cho định lý 4.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Mặt phẳng Q xác định bởi 2 điểm chuyển động tự do trong không gian và luôn vuông góc với mặt phẳng P. Đuờng thẳng a đi qua 2 điểm tự do này. Điểm O chuyển động trên đường thẳng a.
Hai đường thẳng phân biệt a, b cắt nhau tại O, xác định mp(Q) vuông góc với mp(P).
Giả sử có mp(Q') khác với (Q) cũng đi qua a và cũng vuông góc với (P). Theo định lý 3 ta có giao tuyết a của (Q) và (Q') phải vuông góc với (P'), điều này trái với giả thiết "a không vuông góc với (P)”. Vậy (Q') trùng với (Q).
4. Hình lăng trụ đứng.
Hình 72a. Hình lăng trụ.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Điểm A có thể chuyển động tự do theo chiều ngang cũng như thẳng đứng. Các đỉnh khác của mặt trên hình lăng trụ có thể chuyển động trong mặt phẳng nằm ngang. Các cạnh bên hình lăng trụ luôn song song với đường thẳng l.
Định nghĩa. Một hình lăng trụ được gọi là lăng trụ đứng nếu các cạnh bên của nó vuông góc với các mặt đáy
Hình 72b. Hình lăng trụ đứng.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Điểm A có thể chuyển động tự do theo chiều ngang cũng như thẳng đứng. Các đỉnh khác của mặt trên hình lăng trụ có thể chuyển động trong mặt phẳng nằm ngang.
Như vậy các mặt bên của hình lăng trụ đứng là những hình chữ nhật và các mặt bên đều vuông góc với mặt đáy.
• Một hình lăng trụ có đáy là miền đa giác đều được gọi là lăng trụ đều
Hình 72c. Hình lăng trụ đều
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Tâm O của mặt trên hình lăng trụ có thể chuyển động theo chiều ngang và chiều thẳng đứng.
Như vậy lăng trụ đều thì có các mặt bên là những hình chữ nhật bằng nhau.
• Một hình lăng trụ đứng có đáy là hình bình hình được gọi là hình hộp đứng.
Như vậy hình hộp đứng có bốn mặt bên là hình chữ nhật, hai mặt đáy là hình bình hành
Hình 73. Hình hộp
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Hình bên trái là hình hộp chữ nhật, có thể dịch chuyển hai điểm A, B để quan sát. Hình bên phải là hình lập phương được xác định bởi tâm O và các đỉnh của hình hộp này
• Một hình hộp đứng có đáy là hình chữ nhật được gọi là hình hộp chữ nhật.
Như vậy, hình hộp chữ nhật có sáu mặt là hình chữ nhật
• Hình hộp có tất cả các mặt đều là hình gọi là hình lập phương
5. Hình chóp đều
Cho hình chóp S. A1A2 . . . An. Gọi H là hình chiếu của S trên mặt đáy, tức SH ⊥ mp(A1A2 . . . An). Khi đó SH gọi là đường cao của hình chóp và H là chân đường cao.
• Một hình chóp được gọi là hình chóp đều nếu đáy của nó là miền đa giác đều và chân đường cao của hình chóp trung với tâm của đa giác đều đó
Hình 74. Hình chóp đều.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Đáy hình chóp đều là một đa giác đều xác định bởi tâm H và các đỉnh. Điểm S có thể dịch chuyển theo phương thẳng đứng.
Ta dễ thấy rằng các cạnh bên của hình chóp đều thì bằng nhau và các mặt bên của nó là những tam giác cân bằng nhau .
Đoạn thẳng nối đỉnh hình chóp với trung điểm một cạnh đáy bất kì gọi là trung đoạn của hình chóp đều.
6. Hình chóp cụt đều
Định nghĩa: Hình chóp cụt được cắt ra từ một hình chóp đều gọi là một hình chóp cụt đều.
Khi đó hai đáy là hai đa giác đều và đồng dạng.
Đường nối tâm OO' của hai đáy gọi là đường cao của hình chóp cụt đều.
Các mặt bên (của hình chóp cụt đều) là những hình thang cân và bằng nhau.
Đoạn thẳng nối trung điểm hai cạnh đáy của hình thang nói trên gọi là trung đoạn của hình chóp cụt đều
Hình 75. Hình chóp cụt đều.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Đáy hình chóp cụt đều là một đa giác đều xác định bởi tâm O và các đỉnh. Tâm O’ của mặt trên có thể chuyển động theo phương thẳng đứng.
7. Các ví dụ.
Ví dụ : Cho hình chóp S. ABC có đáy là tam giác vuông tại C, mặt bên SAC là tam giác đều và năm trong mặt phẳng vuông góc với mặt phẳng (ABC).
a) Chứng minh mp(SBC) ⊥ mp(SAC).
b) Gọi I là trung điểm của SC, chứng minh rằng mp(ABI) ⊥ mp(SBC).
Giải.
Hình 76. Minh họa cho ví dụ 1.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Tam giác ABC vuông tại C. Mặt phẳng SAC luôn vuông góc với mặt phẳng ABC. Tam giác SAC là đều. Các điểm H, I là trung điểm của AC và SC.
Chỉ có thể dịch chuyển các điểm A, B, C trên mặt phẳng (màu xanh).
a) Ta có BC ⊥ AC và (BAC) ⊥ (SAC) nên BC ⊥ (SAC).
Từ đó suy ra
(SAC) ⊥ (SAC)
b) Vì BC ⊥ (SAC) và AI ⊂ (SAC) nên AI ⊥ BC (1)
Vì ΔSAC là tam giác là SI = IC, nên AI ⊥ SC (2)
Từ (1) và (2) ta có
AI ⊥ (SBC)
Vậy (AIB) ⊥ (SBC)
Ví dụ 2. Cho hình chóp tứ giác đều S. SBCD có cạnh bên và cạnh đáy đều bằng a.
a) Tính độ dài đường cao của hình chóp
b) Gọi M là trung điểm của SC, Chứng minh mp(MBD) ⊥ mp(SAC).
Giải.
Hình 77. Minh họa cho ví dụ 2.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
SABCD là hình chóp tứ giác đều. ABCD là hình vuông. S chỉ có thể chuyển động theo phương thẳng đứng. Muốn dịch chuyển và thay đổi hình vuông đáy hãy nháy và rê chuột tại tâm O hoặc tại các đỉnh của hình vuông này.
a) Gọi O là tâm của hình vuông ABCD, do S.ABCD là hình chóp đều nên ta có SO⊥(ABCD).
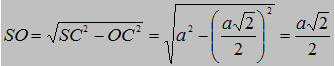
Vậy độ dài đường cao của hình chóp đều S. ABCD là
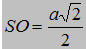
b) Ta có
BS = BC = a và MS = MC. Suy ra
BM ⊥ SC. (1)
Tương tự ta có.
DM ⊥ SC. (2)
Từ (1) và (2) ta suy ra SC ⊥ (BDM).
Vậy (SAC) ⊥ (BDM).
CÂU HỎI BÀI TẬP
1. Cho hai mặt phẳng (P), (Q) cắt nhau, và một điểm M. Chứng minh rằng qua M có một và chỉ một mp(R) vuông góc với (P) và (Q).
Nếu (P)//(Q) kết quả trên thay đổi như thế nào?
2. Trong mp(P) cho tam giác ABC vuông ở B. Một đoạn thẳng AD vuông với (P). Chứng minh rằng mp (ABD) ⊥ mp (BCD).
3. Chứng minh rằng rất cả những mặt phẳng đi qua một điểm A cho trước và vuông góc với một mặt phẳng (P) cho trước đều đi qua mọt đường thẳng cố định.
4. Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a.
SA = SB = SC = a. Chứng minh :
a) mp(ABCD) ⊥ mp(SBD)
b) Tam giác SBD là tam giác vuông.
5. Cho hình hộp chữ nhật ABCD. A'B'C'D' có AB =a, BC =b, CC' = c. Chứng minh rằng các đường chéo của hình hộp đó bằng nhau và bằng 
6. Tính đường chéo của hình lập phương cạnh bằng a.
7. Cho hình lập phương ABCD. A'B'C'D’. Chứng minh rằng AC' ⊥ mp (A'BD), AC'⊥mp (CB'D').
8. Cho tam giác đều ABC cạnh a, I là trung điểm của BC, D là điểm đói xứng của A qua I. Dựng đoạn 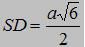 vuông góc với (ABC). vuông góc với (ABC).
Chứng minh:
a) mp(SAB) ⊥ mp(SAC)
b) mp(SBC) ⊥ mp(SAD).
School@net
|

 Xem giỏ hàng
Xem giỏ hàng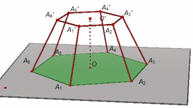 1. Nhận xét.
1. Nhận xét. 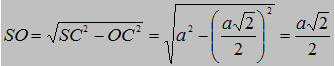
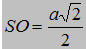

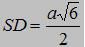 vuông góc với (ABC).
vuông góc với (ABC). 

