Hình 78. Khoảng cách từ một điểm đến một đoạn thẳng.
Đường thẳng a xác định bởi 2 điểm chuyển động tự do trong không gian là M và N. Điểm O cũng có thể chuyển động tự do trong không gian. Trên hình vẽ thể hiện khoảng cách từ O đến đường thẳng a.
Độ dài của đoạn OH được gọi là khoảng cách từ điểm O tới đường thẳng a. Hiển nhiên là:
a) Khoảng cách từ điểm O tới đường thẳng a là bé nhất so với khoảng cách từ O đến mọi điểm của a.
b) Khoảng cách từ điểm O tới đường thẳng a bằng 0 tới đường thẳng a bằng 0 khi và chỉ khi O ∈ a.
2. Khoảng cách từ một điểm tới một mặt phẳng.
Cho một điểm O và một mặt phảng (P). Gọi H là hình chiếu của O trên mp(P)
Hình 79. Khoảng cách từ một điểm đến một mặt phẳng.
Điểm O chuyển động tự do trong không gian. Điểm M chuyển động tự do trên mặt phẳng P.Độ dài đoạn thẳng OH được gọi là khoảng cách từ điểm O tới mp(P).
Hiển nhiên là:
a) Khoảng cách từ điểm O tới mp(P) là bé nhất so với khoảng cách từ O tới mọi điểm của mp(P).
b) Khoảng cách từ điểm O tới mp(P) bằng 0 khi và chỉ khi O nằm trên mp(P).
3. Khoảng cách giữa một đường thẳng và một mặt phẳng song song.
Cho đường thẳng a song song với mp(P)
Hình 80. Khoảng cách giữa một đường thẳng và một mặt phẳng.
Đường thẳng a luôn song song với mặt phẳng P. Điểm A chuyển động tự do trong không gian. Điểm B chuyển động tự do theo phương nằm ngang.
Lấy hai điểm A, B bất kì của a và gọi A', B' là hình chiếu của chúng trên mp(P), Thì ABB'A' là hình chữ nhật, nên AA' = BB'.
Như vậy: Khoảng cách từ một điểm bất kì của đường thẳng a đến mp(P) có giá trị không đổi. Giá trị đó được gọi là khoảng cách từ đường thẳng a tới mp(P).
Hiển nhiên là khoảng cách từ đường thẳng a tới mp(P) là bé nhất so với khoảng cách từ một điểm bất kì của a tới một điểm bất kì của mp(P). (Chú ý rằng ta vẫn giả thiết a // (P)).
4. Khoảng cách giữa hai mặt phẳng song song.
Cho hai mặt phẳng song song (P) và (Q). Ta dễ thấy rằng khoảng cách từ một điểm của mp(P) tới mp(Q) không phụ thuộc vào vị trí của điểm đó
Hình 81. Khoảng cách giữa hai mặt phẳng song song.
Ba điểm A, B, C chuyển động tự do trên mặt phẳng P.
Khoảng cách ấy được gọi là khoảng cách giữa hai mặt phẳng (P) và (Q).
Nó là bé nhất so với khoảng cách giữa một điểm bất kì của (P) với một điểm bất kì của (Q).
5. Đường vuông góc chung của hai đường thẳng chéo nhau.
Định lý: Cho hai đường thẳng chéo nhau a và b, luôn luôn có duy nhất một đường thẳng Δ cắt cả a và b, và vuông góc với mỗi đường thẳng ấy. Đường thẳng Δ đó được gọi là đường vuông góc chung của a và b.
Chứng minh: Gọi (Q) là mặt phẳng đi qua b và song song với a
Hình 82. Minh họa cho định lý về đường vuông góc chung giữa hai đường thẳng trong không gian.
Hai đường thẳng a, b xác định bởi các điểm A, A’ và B, B’ đều có thể chuyển động tự do trong không gian. Đường vuông góc chung MN được xác định một cách duy nhất giữa chúng.
Gọi a' là hình chiếu vuông góc của a lên (Q).
Vì a // (Q) nên a // a', bởi vậy a' và b phải cắt nhau tại một điểm N. Gọi Δ là đường thẳng đi qua N và vuông góc với (Q) thì Δ nằm trong (R) nên Δ cắt a ở điểm M. Rõ ràng Δ là đường thẳng cắt cả a và b, vuông góc với cả a và b.
Giả sử có một đường thẳng Δ' khác với Δ, Δ' cắt cả a và b và Δ' vuông góc với cả a và b, suy ra Δ' ⊥ mp(Q) nên Δ' //Δ, như vậy a và b cùng thuộc mặt phẳng xác định bởi Δ và Δ' điều này trái với giả thiết a, b chéo nhau. Vậy đường vuông góc chung Δ cua a bà ba duy nhất.
6. Khoảng cách giữa hai đường thẳng chéo nhau.
Định nghĩa: Giả sử a, b là hai đường thẳng chéo nhau, đường vuông góc chung của chúng cắt a và b lần lượt tại M và N
Hình 83. Khoảng cách giữa hai đường thẳng chéo nhau.
Các đường thẳng a, b có thể chuyển động tự do trong không gian. Các điểm M, N được xác định duy nhất.
Đoạn MN được gọi là đoạn vuông góc chung của a và b. Độ dài đoạn thẳng MN được gọi là khoảng cách giữa MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.
Nếu gọi (P) và (Q) là hai mặt phẳng song song với nhau lần lượt đi qua a và b thì rõ ràng là độ dài đoạn thẳng MN cũng là khoảng cách giữa đường thẳng a và mp(Q), cũng là khoảng cách giữa đường thẳng b và mp(P), cũng là khoảng cách giữa hai mặt phẳng (P) và (Q)
Hình 84. Minh họa cho việc tính khoảng cách giữa hai đường thẳng chéo nhau.
Các đường thẳng a, b có thể chuyển động tự do trong không gian. Các điểm M, N được xác định duy nhất theo cách dựng của SGK.
Như vậy ta có các tính chất:
1) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó chứa đường thẳng còn lại.
2) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song và lần lượt chứa hai đường thẳng đó.
Từ đó suy ra:
3) Khoảng cách giữa hai đường thẳng chéo nhau là bé nhất so với khoảng cách giữa hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy.
7. Các ví dụ
Ví dụ 1: Cho tứ diện OABC, trong đó OA, OB, OC đôi một vuông góc và OA = OB = OC = a. Gọi I là trung điểm của BC. Hãy xác định và tính độ dài đoạn vuông góc chung của các cặp đường thẳng:
a) OA và BC
b) AI và OC.
Giải.
Hình 85. Minh họa cho ví dụ 1.
Các đoạn thẳng OA, OB, OC đôi một vuông góc với nhau và bằng nhau.
Vì OA, OB, OC đôi một vuông góc nên OA ⊥ (OBC), OC ⊥ (OBA); OB⊥(OAC).
a) Ta có
OA ⊥ (OBC)
nên OA ⊥ OI.
Tam giác OBC cân và
IB = IC nên OI ⊥ BC.
Vậy OI là đoạn vuông góc chung của OA và BC.
Và 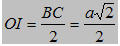
b) Gọi J là trung điểm của OB, H là hình chiếu của O lên AJ, qua H kẻ đường thẳng song song với OC và cắt AI tại E, qua E kẻ đường thẳng song song với OH và cắt OC tai F.
Ta có OC ⊥ (OAB) nên OC ⊥ OH.
Vì I, J lần lượt là trung điểm của BC, OB nên IJ//OC, do đó
IJ ⊥ OH.
Ta lại có OH ⊥ AJ nên OH ⊥ AI
Vì EF // OH nên EF⊥OC và EF ⊥ AI.
Vậy EF là đoạn vuông gó chung của OC và AI.
Ta có EF = OH.
Trong tam giác vuông AOJ ta có:
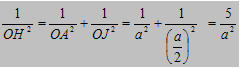
Nên 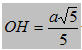
Vậy 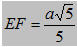
Ví dụ 2. Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với đáy và SA = a. Tính khoảng cách giữa hai đường thẳng:
a) SC và BD
b) AC và SD.
Giải.
Hình 86. Minh họa cho ví dụ 2.
Đáy ABCD luôn là hình vuông. SA vuông góc với đáy.
a) Gọi O là tâm của hình vuông ABCD, H là hình chiếu của O xuống SC ta có:
nên BD ⊥ OH
Mặt khác OH ⊥ SC vậy OH là đoạn vuông góc chung của SC và BD.
Hai tam giác vuông SAC và OHC có góc nhọn C chung nên đồng dạng. Từ đó suy ra:
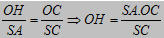
SA=a
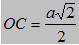

Do đó 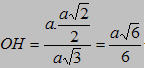
Vậy khoảng cách giữa SC và BD là 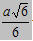
b) Kẻ Dt //AC thì ta có AC // mp(S, Dt) nên khoảng cách giữa AC và SD cũng chính là khoảng cách giữa AC và mp(S, Dt). Kẻ AI ⊥ Dt, AE ⊥ SI. Vì Dt//AC nên Dt⊥SA do đó Dt ⊥ (SAI). Vì AE ⊂ (SAI) nên Dt ⊥ AE từ đó ta có AE ⊥ mp(S, Dt) vậy AE là khoảng cách cần tìm.
Ta có: 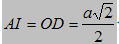
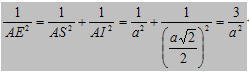 Nên
Nên 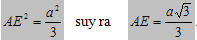
Vậy khoảng cách giữa AC và SD là 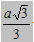
CÂU HỎI VÀ BÀI TẬP
1. Cho hình lập phương ABCD. A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm B, C, D, A', B', D' tới đường chéo AC' bằng nhau. Tính khoảng cách đó.
2. Cho hình chữ nhật ABCD. A'B'C'D' có AB = a, BC = b, CC= c.
a) Tính khoảng cách từ B tới mp(ACC'A').
b) Tính khoảng cáh giữa hai đường thưảng BB' và AC'.
3. Cho hình lập phương ABCD. A'B'C'D'.
a) Chứng minh rằng B'D' ⊥ mp(BA'C'), B'D ⊥mp(ACD')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'.
4. Cho tứ diên ABCD với AC = BD, AD = BC. Chứng minh rằng đường thẳng nối trung điểm hai cạnh AB và CD là đường vuông góc chung của hai đường thẳng AB và CD.
5. Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD, DA = BC.
6. Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a.
7. Hình chóp S. ABCD có ABCD là hình vuông cạnh a, SA vuông góc với đáy của ABCD và SA = a. Xác định và tính độ dài đoạn vuông góc chung của các cặp đường thẳng:
a) SB và AD
b) SC và BD
c) SB và CD
8. Hình chóp S. ABCD có ABCD là hình vuông cạnh a và 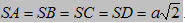 Gọi I và J lần lượt là trung điểm của AD và BC. Gọi I và J lần lượt là trung điểm của AD và BC.
a) Chứng minh mặt phẳng (SIJ) vuông góc với mặt phẳng (SBC).
b) Tính khoảng cách giữa hai đường thẳng AD và SB.
School@net
|

 Xem giỏ hàng
Xem giỏ hàng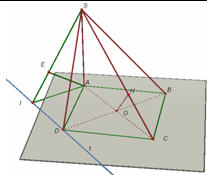 1. Khoảng cách từ một điểm tới một đường thẳng.
1. Khoảng cách từ một điểm tới một đường thẳng. 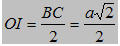
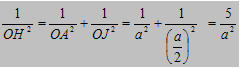
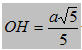
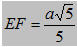
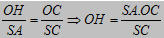
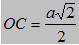

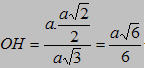
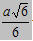
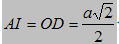
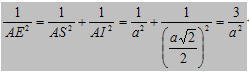 Nên
Nên 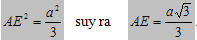
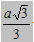
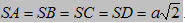 Gọi I và J lần lượt là trung điểm của AD và BC.
Gọi I và J lần lượt là trung điểm của AD và BC. 

