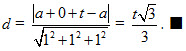| Cong ty Cong Nghe Tin hoc Nha truong | http://www.schoolnet.vn |
| Toán 12- Nâng Cao - Chương III - Bài 2. PHƯƠNG TRÌNH MẶT PHẲNG 18/11/2011 §2 PHƯƠNG TRÌNH MẶT PHẲNG 1. Phương trình mặt phẳng Vectơ Rõ ràng nếu
Hình 63 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch3_h63.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Nhận xét. Nếu ta đặt D = -(Ax0 + By0 + Cz0) thì phương trình (1) trở thành : Ax + By + Cz + D = 0, trong đó A2 + B2 + C2>0. (2) Phương trình (2) gọi là phương trình tổng quát của mặt phẳng (α) hay nói gọn là phương trình mp(α). Như vậy, ta đễ dàng viết được phương trình mặt phẳng nếu biết tọa độ của một điểm thuộc nó và tọa độ một vectơ pháp tuyến của nó.
-4(x - 0) – 2(y – 1) + 2(z - 1) = 0 hay 2x + y +z = 0. ¢ 1 Trong không gian Oxyz, cho hai điểm A(1 ; -2 ; 3) và B(-5 ; 0 ; 1). Hãy viết phương trình mặt phẳng trung trực(P) của đoạn thẳng AB. Như vậy, mỗi mặt phẳng đều có phương trình dạng (2). Định lý sau đây khẳng định điều ngược lại.
Lấy một nghiệm (x0 ;y0 ; z0) và vectơ pháp tuyến là
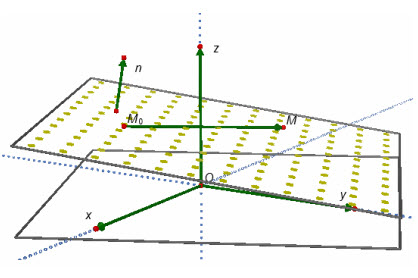
Trong không gian Oxyz, xét mặt phẳng (α) có phương trình : Ax + By + Cz + D = 0 Hãy giải thích vì sao ta có các khẳng đình sau đây : a) Mặt phẳng (α) đi qua gốc tọa độ O khi và chỉ khi D = 0.
Hãy phát biểu kết luận tương tự cho trường hợp B = 0 và trường hợp C = 0.
Hãy phát biểu kết luận tương tự cho trường hợp B = C = 0 và trường hợp C = A = 0. Sau đây ta xét trường hợp mặt phẳng có phương trình Ax + By + Cz + D = 0 với cac hệ số A, B, C, D đều khác 0. Khi đó bằng cách đặt
Rõ ràng mặt phẳng có phương trình(3) cắt trục Ox, Oy, Oz lần lượt tại các điểm M(a ; 0 ; 0), N(0 ; b ; 0) và P(0 ; 0 ; c). Độ dài đại số của các vectơ
b) Tìm tọa độ hình chiếu H của điểm O trên mp(α).
a) Các hình chiếu của M trên các trục tọa độ là các điểm (30 ; 0 ; 0), (0 ; 15 ; 0) và (0 ; 0 ; 6). Phương trình mp(α) đi qua ba điểm đó là
Bằng cách thay các giá trị x, y, z từ ba phương trình cuối vào phương trình đầu, ta được t + 4t + 25t – 30 = 0. Từ đó ta tìm được t = 1 và do đó H = (1 ; 2 ; 5).¢
Xét các bộ n số (x1 ; x2 ; … ; xn) (n>2), trong đó các số x1, x2, …, xn không đồng thời bằng 0. • Hai bộ số (A1 ; A2 ; … ; An) và (B1 ; B2 ; … ; Bn) như thế được gọi là tỉ lệ với nhau (hay tỉ lệ) nếu có một số t sao cho A1 = tB1, A2 = tB2,…, An = tBn. Khi đó ta viết
Theo định nghĩa đó, ta có
A1 : A2 : … : An≠B1 : B2 : … : Bn .
1 : 0 : 1 : 2≠ 1 : 1 : 1 : 2. • Ta hãy xét trường hợp hai bộ số (A1 ; A2 ;… ; An) và (B1 ; B2 ;… ; Bn) tỉ lệ, nhưng hai bộ số (A1 ; A2 ;… ; An ;An+1) và (B1 ; B2 ;… ; Bn ; Bn+1) không tỉ lệ. Điều đó có nghĩa là : có số t sao cho A1 = tB1, A2 = tB2,…, An = tBn nhưng An+1 ≠tBn+1 . Trong trường hợp đó, ta viết :
(α) : Ax + By + Cz + D = 0 (α') : A'x + B'y + C'z + D’ = 0 ; Chúng lần lượt có vectơ pháp tuyến là
Bây giờ xét trường hợp A : B : C =A' : B' : C' hay
Hãy xét vị trí tương đối giữa hai mặt phẳng (α)và (α') trong mỗi trường hợp sau :
Cho hai mặt phẳng (α)và (α') lần lượt có phương trình : (α) : Ax + By + Cz + D = 0 (α') : A'x + B'y + C'z + D’ = 0. a) Hai mặt phẳng đó cắt nhau khi và chỉ khi A : B : C ≠ A' : B' : C' . b) Hai mặt phẳng đó song song khi và chỉ khi
c) Hai mặt phẳng đó trùng nhau khi và chỉ khi
Cho hai mặt phẳng (α) : 2x – my + 10z + m +1 = 0 (β) : x – 2y + (3m +1)z – 10 = 0. Hãy tìm giá trì của m để : a) Hai mặt phẳng đó song song ; b) Hai mặt phẳng đó trùng nhau ; c) Hai mặt phẳng đó cắt nhau ; d) Hai mặt phẳng đó vuông góc với nhau.
Tính khoảng cách giữa hai mặt phẳng có phương trình lần lượt là : 3x – y + 2z – 6 = 0 và 6x – 2 y + 4z + 4 = 0.
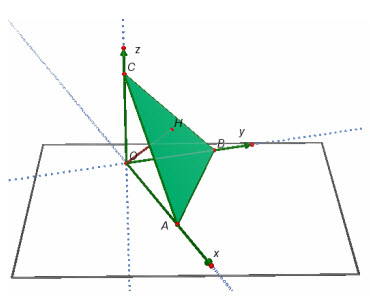
Vì ba cạnh OA,
Hình 64 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch3_h64.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Khi đó mp(ABC) có phương trình theo đoạn chắn là
Chiều cao h cần tìm là khoảng cách từ điểm O tới mp(ABC) nên
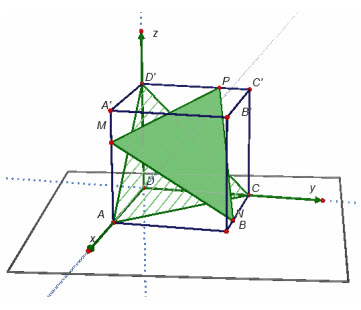
Chọn hệ tọa độ Oxyz, có gốc O trùng với D, các trục Ox, Oy, Oz lần lượt đi qua A, C', D' như ở hình 65.
Hình 65 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch3_h65.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Khi đó : A = (a ; 0 ; 0), C = (0 ; a ; 0), D' = (0 ; 0 ; a), M = (a ; 0 ; t), N = (t ; a ; 0), P = (0 ; t ; a).
Mặt khác, mp(MNP) có vectơ pháp tuyến là Ta có Từ đó ta tìm được tọa độ của vectơ
a) Đi qua ba điểm M(2 ; 0 ; -1), N(1 ; -2 ; 3), P(0 ; 1 ; 2) ; b) Đi qua hai điểm A(1 ; 1 ; -1), B(5 ; 2 ; 1) và song song với trục Oz ; c) Đi qua hai điểm (3 ; 2 ; -1) và song song với mặt phẳng có phương trình x – 5y + z = 0 ; d) Đi qua hai điểm A(0 ; 1 ; 1), B(-1 ; 0 ; 2) và vuồn góc với mặt phẳng x – y + z + 1 = 0 ; e) Đi qua điểm M(a ; b ; c) (với abc ≠ 0) và song song với một mặt phẳng tọa độ ; g) Đi qua điểm G(1 ; 2 ; 3) và cắt các trục tọa độ tại các điểm A ; B ; C sao cho G là trọng tâm tam giác ABC ; h) Đi qua điểm H(2 ; 1 ; 1) và cắt các trục tọa độ tại các điểm A, B, C sao cho H là trực tâm của tam giác ABC.
a) x + 2y – z + 5 = 0và 2x + 3y – 7z - 4 = 0 ; b) x + 2y – z - 3 = 0và 2x - y + 4z - 2 = 0 ; c) x + y + z - 1 = 0và 2x + 2y +2z + 3 = 0 ; d) 3x - 2y + 3z + 5 = 0và 9x - 6y – 9z - 5 = 0 ; e) x - y + 2z - 4 = 0và 10x - 10y + 20z - 40 = 0 .
a) 2x + my + 2z +3 = 0và mx + 2y – 4z + 7 = 0 ; b) 2x + y + mz - 2 = 0và x + n y + 2z + 8 = 0 .
2x – my + 3z – 6 + m = 0 và(m + 3)x – 2y + (5m + 1)z – 10 = 0. Với giá trì nào của m thì : a) Hai mặt phẳng đó song song ; b) Hai mặt phẳng đó trùng nhau ; c) Hai mặt phẳng đó cắt nhau ; d) Hai mặt phẳng đó vuông góc ?
a) (α) : 2x – y + 4z + 5 = 0, (α’) : 3x + 5y – z – 1 = 0 ; b) (α) : 2x + y - 2z - 1 = 0, (α’) : 6x - 3y + 2z – 2 = 0 ; c) (α) : x + 2y + z - 1 = 0, (α’) : x + 2y + z + 5 = 0 ;
Ax + By + Cz + D = 0 và Ax + By + Cz + D' = 0 với D ≠ D'.
a) M cách đều điểm A(2 ; 3 ; 4) và mặt phẳng 2x + 3y + z - 17 = 0 ; b) M cách đều hai mặt phẳng x + y - z + 1 = 0 và x - y + z + 5 = 0.
a) Tam giác ABC có ba góc nhọn ; b) cos2α + cos2β + cos2γ = 1.
x2 + y2+ z2 – 2x – 4y - 6z – 2 = 0. |
| URL của bài viết này::http://www.schoolnet.vn/modules.php?name=News&file=article&sid=5795 |
| © Cong ty Cong Nghe Tin hoc Nha truong | contact: sales@schoolnet.vn |
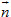 ≠ 0 gọi là vectơ pháp tuyến của mặt phẳng (α) nếu giá của
≠ 0 gọi là vectơ pháp tuyến của mặt phẳng (α) nếu giá của 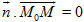
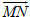 = (1 ; -3 ; -1) và
= (1 ; -3 ; -1) và 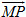 = (1 ; -1 ; 1). Từ đó ta tính được
= (1 ; -1 ; 1). Từ đó ta tính được 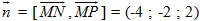 . Vectơ
. Vectơ 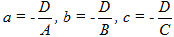
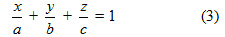
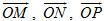 trên các trục tọa độ chứa chúng lần lượt là
trên các trục tọa độ chứa chúng lần lượt là 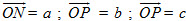 . Bởi vậy phương trình (3) được gọi là phương trình mặt phẳng theo đoạn chắn.
. Bởi vậy phương trình (3) được gọi là phương trình mặt phẳng theo đoạn chắn.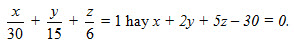
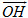 cùng phương với vectơ pháp tuyến
cùng phương với vectơ pháp tuyến 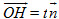 . Bởi vậy, nếu gọi (x, y, z) là tọa độ của H thì
. Bởi vậy, nếu gọi (x, y, z) là tọa độ của H thì 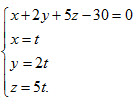
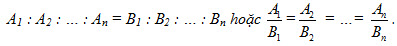
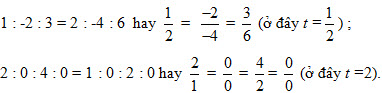
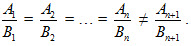
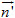 (A' ; B' ; C').
(A' ; B' ; C').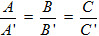

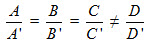
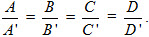
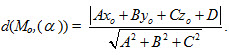
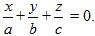
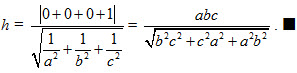
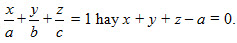
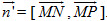 .
.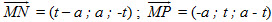 .
.