Giả sử điểm M có tọa độ (x, y). Khi đó  2. Tích vô hướng của hai vectơ - Tích vô hướng của hai vectơ 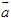 và và 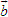 là là 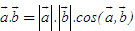 . . - Các tính chất 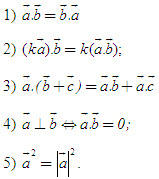 - Biểu thức tọa độ của tích vô hướng và khoảng cách giữa hai điểm 1) Nếu 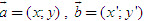 thì thì 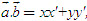 2) Nếu M(xM; yM),N(xN ; yN) thì 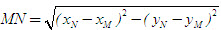 3. Định lí côsin trong tam giác a2 = b2 + c2 – 2bc cosA. 4. Định lí sin trong tam giác 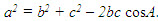 . . 5. Công thức trung tuyến của tam giác 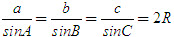 . .
6. Các công thức tính diện tích tam giác 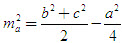 . . II – Câu hỏi tự kiểm tra 1. Phát biểu định nghĩa tích vô hướng của hai vectơ. Khi nào thì tích vô hướng của hai vectơ là số dơng, là số âm, bằng 0 ? 2.Để giải tam giác ta thường dùng định lí côsin trong những trường hợp nào? Dùng định lí sin trong những trường hợp nào? 3. Cho biết độ dài 3 cạnh của tam giác. Làm thế nào để tính a) Các góc của tam giác? b) Các đường cao của tam giác? c) Bán kính đường tròn ngoại tiếp và nội tiếp tam giác? d) Diện tích tam giác? 4. Trong mặt phẳng tọa độ, cho biết tọa độ ba đỉnh của tam giác, làm thế nào để tìm chu vi, diện tích, tọa độ trực tâm, tâm đường tròn ngoại tiếp tam giác? III – Bài tập 1. Chứng minh các công thức sau a) 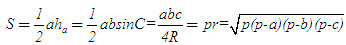 ; ; b) 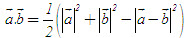 . .
2. Gọi G là trọng tâm tam giác ABC. a) Chứng minh rằng với mọi điểm M, ta luôn có MA2+ MB2 + MC2 = 3MG2 + GA2 + GB2+ GC2. b) Tìm tập hợp các điểm M sao cho MA2 + MB2+ MC2 = k2, trong đó k là một số cho trước. 3. Cho hình bình hành ABCD. Tìm tập hợp các điểm Msao cho MA2 + MB2 + MC2+ MD2= k2, Trong đó klà một số cho trước. 4. Trên hình 63 vẽ hai tam giác vuông cân ABCvà AB’C’ có chung đỉnh A. Gọi I, Jlần lượt là trung điểm của hai đoạn thẳng BB’ và CC’ a) Chứng minh rằng 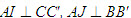 ; ; b) 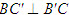 . . 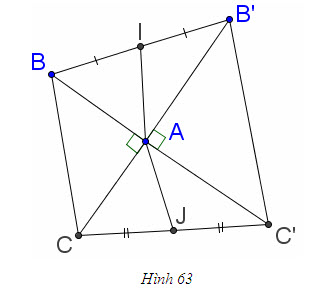 Tải trực tiếp tệp hình học động: L10_nc_ch2_h63.ggb Xem trực tiếp hình vẽ động trên màn hình. 5. Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD, Mlà điểm trên AC sao cho 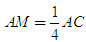 . . a) Tính các cạnh của tam giác BMN. b) Có nhận xét gì về tam giác BMN ? Tính diện tích tam giác đó. c) Gọi Ilà giao điểm của BN và AC. Tính CI. d) Tính bán kính đường tròn ngoại tiếp tam giác BDN. 6. Trong mặt phẳng tọa độ, cho 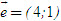 và và 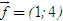 . . a) Tìm góc giữa các vectơ 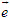 và và 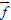 . . b) Tìm mđể vectơ 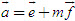 vuông góc với trục hoành. vuông góc với trục hoành. c) Tìm nđể vectơ 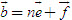 tạo với vectơ tạo với vectơ 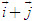 một góc 45o/ một góc 45o/ 7. Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ Bvà C vuông góc với nhau là b2+ c2 = 5a2. 8. Trong các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất. 9.Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S, chiều cao ha, các bán kính R, r của đường tròn ngoại tiếp, nội tiếp tam giác đó. 10. Cho tam giác ABC. Chứng minh rằng a) 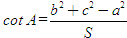 (S là diện tích tam giác ABC); (S là diện tích tam giác ABC); b) 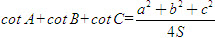 . . 11.Cho hai đường tròn (O ; R) và (O’ ; R’) cắt nhau tại hai điểm A và B. Trên đường thẳng AB, lấy điểm C ở ngoài hai đường tròn và kẻ hai tiếp tuyến CE, CF đến hai đường tròn đó (E, F là các tiếp điểm). Chứng minh rằng CE = CF. 12.Cho đường tròn (O ; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau. a) Chứng minh rằng AB2 + CD2 không đổi. b) Chứng minh rằng PA2 + PB2 + PC2 + PD2không phụ thuộc vào vị trí của điểm P. IV – Bài tập trắc nghiệm 1. Giá trị cos45o + sin45o bằng bao nhiêu?  2. Trong các đẳng thức sau, đẳng thức nào đúng? (A) sin(180o - α) = - cosα ; (B) sin(180o - α) = - sinα ; (C) sin(180o - α) = sinα ; (D) sin(180o - α) = cosα ; 3. Trong các đẳng thức sau, đẳng thức nào sai ? (A) sin0o + cos0o = 0; (B) sin90o + cos90o = 1; (C) sin180o + cos180o = -1; (D) 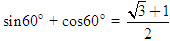 ; ; 4. Trong các hệ thức sau, hệ thức nào không đúng? (A) 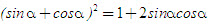 ; ; (B) 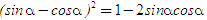 ; ; (C) 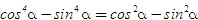 ; ; (D) 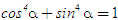 5. Cho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng 120o ?  6. Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai? 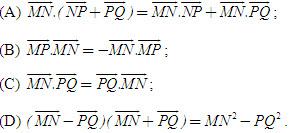 7. Trong các hệ thức sau, hệ thức nào đúng?  8. Trong mặt phẳng tọa độ, cho 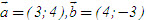 . Kết luận nào sau đây là sai? . Kết luận nào sau đây là sai?  9. Trong mặt phẳng tọa độ, cho 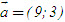 . Vectơ nào sau đây không vuông góc với vectơ . Vectơ nào sau đây không vuông góc với vectơ 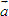 ? ?  10. Tam giác ABC có a = 14, b = 18, c = 20. Kết quả nào sau đây là gần đúng nhất?  11. Nếu tam giác MNP có MP = 5, PN = 8 và 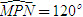 thì độ dài cạnh MN (làm tròn đến chữ số thập phân thứ nhất) là thì độ dài cạnh MN (làm tròn đến chữ số thập phân thứ nhất) là (A) 11,4;(B) 12,4; (C) 7,0;(D) 12,0. 12. Cho tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE, EPF, FPQ bằng nhau. Đặt MP = q, PQ = m, PE = x. PF = y (h. 64). 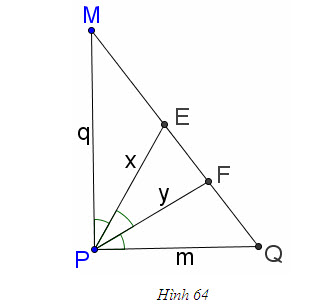 Tải trực tiếp tệp hình học động: L10_nc_ch2_h64.ggb Xem trực tiếp hình vẽ động trên màn hình. Trong các hệ thức sau, hệ thức nào đúng? (A) ME = EF = FQ; (B) ME2= q2 + x2 – xq; (C) MF2= q2 + y2 – yq; (D) MQ2= q2 + m2 – 2qm. 13.Tam giác ABC có BC = 10, 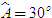 . Bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu? . Bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?  14. Tam giác với ba cạnh là 5, 12 và 13 có diện tích bằng bao nhiêu?  15. Tam giác ABC có ba cạnh là 6, 10, 8. Bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu?  ; ; 16. Tam giác ABC có 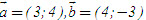 , AB = 5. Hỏi cạnh AC bằng bao nhiêu? , AB = 5. Hỏi cạnh AC bằng bao nhiêu? 
School@net
|

 Xem giỏ hàng
Xem giỏ hàng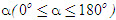 , ta xác định điểm M trên nửa đường tròn đơn vị sao cho
, ta xác định điểm M trên nửa đường tròn đơn vị sao cho 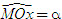 .
.
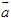 và
và 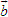 là
là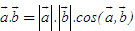 .
.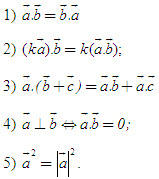
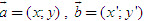 thì
thì 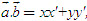
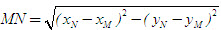
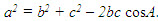 .
.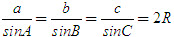 .
.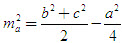 .
.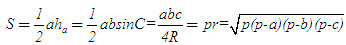 ;
;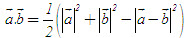 .
.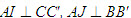 ;
;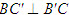 .
.
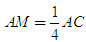 .
.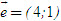 và
và 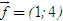 .
.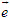 và
và 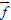 .
.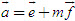 vuông góc với trục hoành.
vuông góc với trục hoành.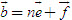 tạo với vectơ
tạo với vectơ 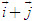 một góc 45o/
một góc 45o/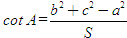 (S là diện tích tam giác ABC);
(S là diện tích tam giác ABC);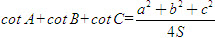 .
.
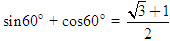 ;
;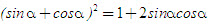 ;
;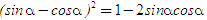 ;
;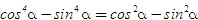 ;
;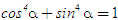

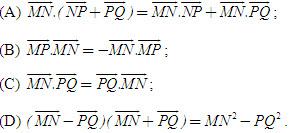

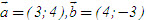 . Kết luận nào sau đây là sai?
. Kết luận nào sau đây là sai?
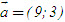 . Vectơ nào sau đây không vuông góc với vectơ
. Vectơ nào sau đây không vuông góc với vectơ 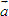 ?
?

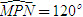 thì độ dài cạnh MN (làm tròn đến chữ số thập phân thứ nhất) là
thì độ dài cạnh MN (làm tròn đến chữ số thập phân thứ nhất) là
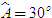 . Bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
. Bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?

 ;
; 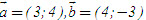 , AB = 5. Hỏi cạnh AC bằng bao nhiêu?
, AB = 5. Hỏi cạnh AC bằng bao nhiêu?


