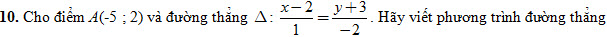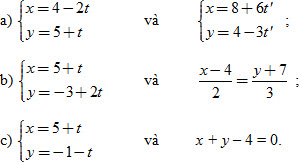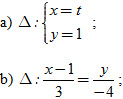
Hình 70
Tải trực tiếp tệp hình học động: L10_nc_ch3_h70.ggb Xem trực tiếp hình vẽ động trên màn hình. ĐỊNH NGHĨA
Vectơ 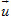 khác khác 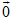 , có giá song song hoặc trùng với đường thẳng Δ được gọi là vectơ chỉ phương của Δ. , có giá song song hoặc trùng với đường thẳng Δ được gọi là vectơ chỉ phương của Δ.
?1. Vectơ chỉ phương và vectơ pháp tuyến của một đường thẳng quan hệ với nhau như thế nào?
?2. Vì sao vectơ 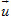 = (b; -a) là một vectơ chỉ phương của đường thẳng có phương trình ax + by + c = 0 ? = (b; -a) là một vectơ chỉ phương của đường thẳng có phương trình ax + by + c = 0 ?
2. Phương trình tham số của đường thẳng
Bài toán. Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ đi qua điểm I(x0 ; y0) và có vectơ chỉ phương 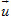 = (b ; a). Hãy tìm điều kiện của x và y để điểm M(x ; y) nằm trên Δ. = (b ; a). Hãy tìm điều kiện của x và y để điểm M(x ; y) nằm trên Δ.
1. (Để giải bài toán)
Điểm M nằm trên Δ khi và chỉ khi vectơ 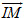 cùng phương với vectơ cùng phương với vectơ 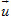 (h. 71), tức là có số t sao cho (h. 71), tức là có số t sao cho

Hãy viết tọa độ của 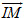 và của t và của t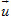 rồi so sánh các tọa độ của hai vectơ này. rồi so sánh các tọa độ của hai vectơ này. 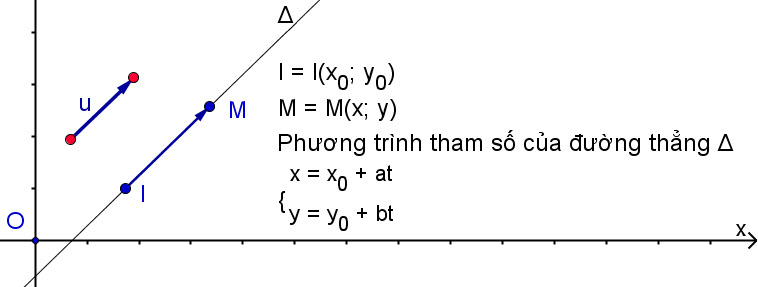
Hình 71
Tải trực tiếp tệp hình học động: L10_nc_ch3_h71.ggb Xem trực tiếp hình vẽ động trên màn hình. Từ hoạt động trên suy ra: Điều kiện cần và đủ để M(x ; y) thuộc Δ là có số t sao cho

Hệ (1) được gọi là phương trình tham số của đường thẳng Δ, với tham số t.
CHÚ Ý:
Với mỗi giá trị của tham số t, ta tính được x và y từ hệ (1), tức là có được điểm M(x ; y) nằm trên Δ. Ngược lại, nếu điểm M(x ; y) nằm trên Δ thì có một số t sao cho x, y thỏa mãn hệ (1).
?3. Cho đường thẳng Δ có phương trình tham số
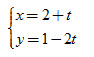
a) Hãy chỉ ra một vectơ chỉ phương của Δ.
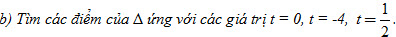
c) Điểm nào trong các điểm sau thuộc Δ?
M(1 ; 3), N(1 ; -5), P(0 ; 1), Q(0 ; 5).
2. Cho đường thẳng d có phương trình tổng quát 2x – 3y – 6 = 0.
a) Hãy tìm tọa độ của một điểm thuộc d và viết phương trình tham số của d.

c) Tìm tọa độ của điểm M thuộc d sao cho OM = 2.
CHÚ Ý:
Trong phương trình tham số 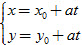 của đường thẳng, nếu a ≠ 0, b ≠ 0 thì bằng cách khử tham số t từ hai phương trình trên, ta đi đến của đường thẳng, nếu a ≠ 0, b ≠ 0 thì bằng cách khử tham số t từ hai phương trình trên, ta đi đến
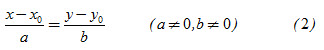
Phương trình (2) được gọi là phương trình chính tắc của đường thẳng.
Trong trường hợp a = 0 hoặc b = 0 thì đường thẳng không có phương trình chính tắc.
Ví dụ. Viết phương trình tham số, phương trình chính tắc (nếu có) và phương trình tổng quát của đường thẳng trong mỗi trường hợp sau
a) Đi qua điểm A(1 ; 1) và song song với trục hoành;
b) Đi qua điểm B(2 ;- 1) và song song với trục tung;
c) Đi qua điểm C(2 ; 1) và vuông góc với đường thẳng d: 5x – 7y + 2 = 0.
Giải. a) Đường thẳng cần tìm có vectơ chỉ phương 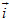 = (1 ; 0) và đi qua A nên có phương trình tham số là = (1 ; 0) và đi qua A nên có phương trình tham số là 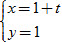 và phương trình tổng quát là y – 1 = 0. và phương trình tổng quát là y – 1 = 0.
Đường thẳng đó không có phương trình chính tắc.
b) Đường thẳng cần tìm có vectơ chỉ phương 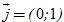 nên không có phương trình chính tắc. Do đường thẳng đó đi qua B nên có phương trình tham số là nên không có phương trình chính tắc. Do đường thẳng đó đi qua B nên có phương trình tham số là 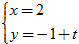 và phương trình tổng quát là x – 2 = 0. và phương trình tổng quát là x – 2 = 0.
c) Vectơ pháp tuyến 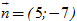 của d cũng là một vectơ chỉ phương của đường thẳng Δ cần tìm (do Δ⊥d). Do đó phương trình tham số của là của d cũng là một vectơ chỉ phương của đường thẳng Δ cần tìm (do Δ⊥d). Do đó phương trình tham số của là 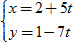 là phương trình chính tắc của Δ là là phương trình chính tắc của Δ là 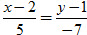 . .
Từ phương trình chính tắc (hoặc tham số) của Δ, ta suy ra được phương trình tổng quát của Δ là 7x + 5y – 19 = 0.
3. Viết phương trình tham số, phương trình chính tắc (nếu có) và phương trình tổng quát của đường thẳng đi qua hai điểm M(-4 ; 3) và N(1 ; -2).
Câu hỏi và bài tập
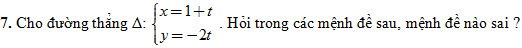
a) Điểm A(-1 ; -4) thuộc Δ.
b) Điểm B(8 ; 14) không thuộc Δ, điểm C(8 ; -14) thuộc Δ.
c) Δ có vectơ pháp tuyến 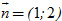 . .
d) Δ có vectơ chỉ phương 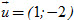 . .
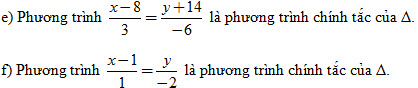
8. Cho đường thẳng : ax + by + c = 0. Trong các mệnh đề sau, mệnh đề nào đúng?
a) Vectơ 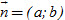 là vectơ pháp tuyến của Δ. là vectơ pháp tuyến của Δ.
b) Δ có vectơ chỉ phương 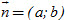 . .
c) Δ có vectơ chỉ phương 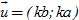 với . với .
d) Δ có vectơ chỉ phương 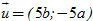 . .
e) Đường thẳng vuông góc với Δ có vectơ chỉ phương 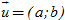 . .
9. Hãy viết phương trình tham số, phương trình chính tắc (nếu có) và phương trình tổng quát của đường thẳng đi qua hai điểm A và B trong mỗi trường hợp sau
a) A = (-3 ; 0) , B = (0 ; 5);
b) A = (4 ; 1) , B = (4 ; 2);
c) A = (-4 ; 1) , B = (1 ; 4);
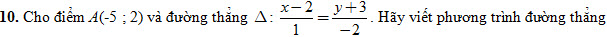
a) Đi qua A và song song với Δ.
b) Đi qua A và vuông góc với Δ.
11. Xét vị trí tương đối của mỗi cặp đường thẳng sau đây và tìm tọa độ giao điểm (nếu có) của chúng
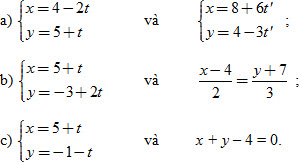
12. Tìm hình chiếu vuông góc của điểm P(3 ; -2) trên đường thẳng Δ trong mỗi trường hợp sau
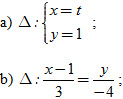
c) Δ: 5x – 12y + 10 = 0 .
13. Trên đường thẳng Δ: x – y + 2 = 0, tìm điểm M cách đều hai điểm E(0 ; 4) và F(4 ; 9).
14. Cho hình bình hành có tọa độ một đỉnh là (4 ; -1). Biết phương trình các đường thẳng chứa hai cạnh là x – 3y = 0 và 2x + 5y + 6 = 0. Tìm tọa độ ba đỉnh còn lại của hình bình hành đó.
School@net
|

 Xem giỏ hàng
Xem giỏ hàng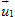 khác
khác 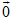 , có giá là đường thẳng Δ; vectơ
, có giá là đường thẳng Δ; vectơ 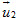 khác
khác 
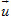 khác
khác 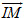 cùng phương với vectơ
cùng phương với vectơ 


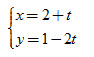

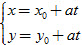 của đường thẳng, nếu a ≠ 0, b ≠ 0 thì bằng cách khử tham số t từ hai phương trình trên, ta đi đến
của đường thẳng, nếu a ≠ 0, b ≠ 0 thì bằng cách khử tham số t từ hai phương trình trên, ta đi đến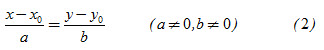
 = (1 ; 0) và đi qua A nên có phương trình tham số là
= (1 ; 0) và đi qua A nên có phương trình tham số là 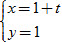 và phương trình tổng quát là y – 1 = 0.
và phương trình tổng quát là y – 1 = 0. nên không có phương trình chính tắc. Do đường thẳng đó đi qua B nên có phương trình tham số là
nên không có phương trình chính tắc. Do đường thẳng đó đi qua B nên có phương trình tham số là 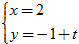 và phương trình tổng quát là x – 2 = 0.
và phương trình tổng quát là x – 2 = 0.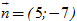 của d cũng là một vectơ chỉ phương của đường thẳng Δ cần tìm (do Δ⊥d). Do đó phương trình tham số của là
của d cũng là một vectơ chỉ phương của đường thẳng Δ cần tìm (do Δ⊥d). Do đó phương trình tham số của là 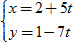 là phương trình chính tắc của Δ là
là phương trình chính tắc của Δ là 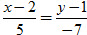 .
.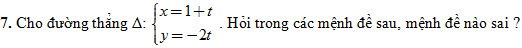
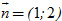 .
.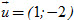 .
.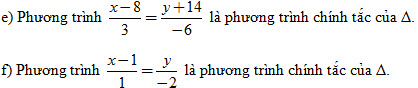
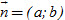 là vectơ pháp tuyến của Δ.
là vectơ pháp tuyến của Δ.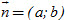 .
.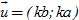 với .
với .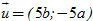 .
.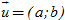 .
.