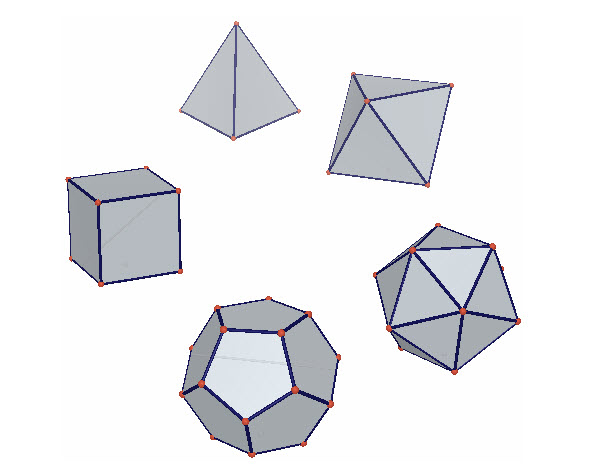
§1 KHÁI NIỆM VỀ KHỐI ĐA DIỆN 1. Khối đa diện. Khối chóp, khối lăng trụ Các em hãy quan sát các hình sau đây (hình 1a, 1b, 1c, 1d, 1e). 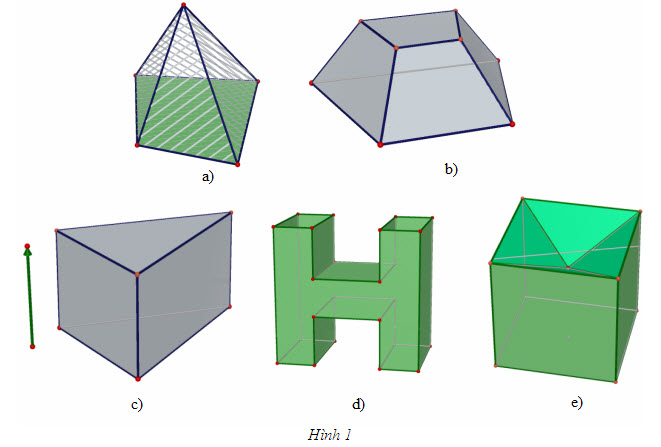
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h1a.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h1b.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h1c.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h1d.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h1e.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Mỗi hình trên đều có hai đặc điểm: a) Gồm một số hữu hạn đa giác phẳng (ở đây “đa giác phẳng” được hiểu là bao gồm cả các điểm trong của nó) ; b) Phân chia không gian thành hai phần: phần bên trong và phần bên ngoài của hình đó. (Nếu ta chế tạo mô hình bằng chất nhựa trong suốt thì ta có thể bơm vào phần bên trong của nó một chất khí có màu, và khi đó phần bên trong đã được “tô màu”, còn phần bên ngoài thì không). Giả sử H là hình có hai đặc điểm nói trên. Khi đó, mỗi điểm thuộc phần bên trong của nó được gọi là điểm nằm trong H. Hình H cùng với các điểm nằm trong Hđược gọi là khối đa diện giới hạn bởi hình H. Mỗi đa giác của hình H được gọi là một mặt của khối đa diện. Các đỉnh, các cạnh của mỗi mặt còn gọi là đỉnh, cạnh của khối đa diện. Các điểm nằm trong hình H còn được gọi là điểm trong của khối đa diện. Khối đa diện còn được gọi là khối chóp, khối chóp cụt nếu nó được giới hạn bởi một hình chóp, hình chóp cụt (h.1a, 1b). Như vậy, ta có thể nói về khối chóp n-giác, khối chóp cụt n-giác, khối chóp đều, khối tứ diện,… . Tương tự, khối đa diện được gọi là khối lăng trụ nếu nó có được giới hạn bởi một hình lăng trụ (h.1c). Ta cũng có thể nói về khối hộp, khối hộp chữ nhật, khối lập phương,… Ngoài các khối kể trên, chúng ta còn gặp các khối đa diện phức tạp hơn như ở các hình 1d, 1e. ?1 Hình hộp chữ nhật H có 6 mặt là hình chữ nhật (h.2a). Nếu ta bỏ đi hình chữ nhật ABCD thì ta được một hình H’chỉ gồm 5 hình chữ nhật (h.2b). Tại sao không thể nói rằng có khối đa diện giới hạn bởi hình H’ ? 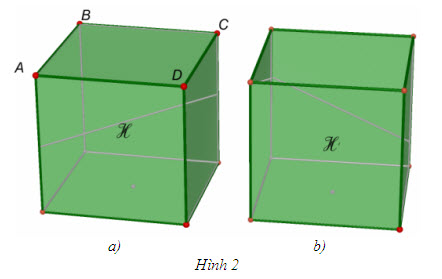
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h2.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Từ đó ta cần chú ý rằng : Khối đa diện được giới hạn bởi một hình gồm những đa giác phẳng, nhưng không phải bất kì hình nào gồm những đa giác phẳng cũng giới hạn ra một khối đa diện. Từ đây trở đi, ta chỉ xét các khối đa diện giới hạn bởi hình H gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện : 1) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung. 2) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác. Hình H gồm các đa giác như thế được gọi là một hình đa diện, hoặc đơn giản là đa diện.  1. 1.
Hãy kiểm tra rằng các hình 1a, 1b, 1c, 1d, 1e đều thỏa mãn các điều kiện 1) và 2) trên đây. Hình 2b không thỏa mãn điều kiện nào trong hai điều kiện đó ? 2. Phân chia và lắp ghép các khối đa diện Ví dụ 1 Cho khối chóp tứ giác S.ABCD (h.3). Ta hãy xét hai khối chóp tam giác S.ABC và S.ACD. 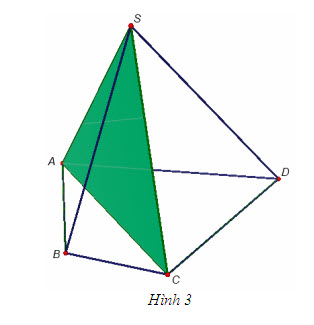
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h3.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Dễ thấy rằng : 1) Hai khối chóp đó không có điểm trong chung, nghĩa là điểm trong của khối chóp này không phải là điểm trong của khối chóp kia. 2) Hợp của hai khối chóp S.ABC và S.ACD chính là khối chóp S.ABCD. Trong trường hợp đó ta nói rằng : Khối đa diện S.ABCD được phân chia thành hai khối đa diện S.ABC và S.ACD. Ta cũng còn nói : Hai khối đa diện S.ABC và S.ACD được ghép lại thành khối đa diện S.ABCD. ?2 Có thể phân chia khối chóp bất kì thành những khối tứ diện hay không ?  2 (h.4) 2 (h.4)
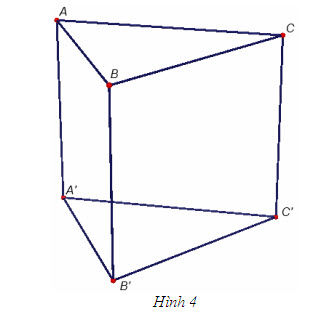
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h4.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) 1) Cắt khối lăng trụ ABC.A’B’C’ bởi mặt phẳng (A’BC). Khi đó khối lăng trụ được chia thành những khối đa diện nào ? 2) Hãy phân chia khối lăng trụ ABC.A’B’C’thành ba khối tứ diện. Một cách tổng quát dễ thấy rằng mọi khối chóp và khối lăng trụ luôn có thể phân chia được thành những khối tứ diện (bằng nhiều cách khác nhau). Thực ra điều đó cũng đúng cho khối đa diện bất kì. Ví dụ 2 Hình 5 cho ta thấy hai miếng gỗ (xem như hai khối đa diện) được chế tạo sao cho chúng có thể ghép vừa khít với nhau để tạo thành một khối lập phương. Để tháo rời hai miếng gỗ ở hình lập phương, cần phải cố định một miếng kia theo một vectơ có phương hoàn toàn xác định. 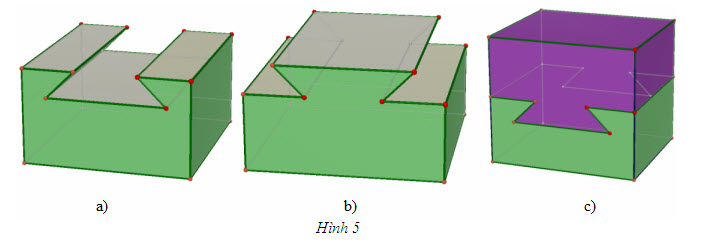
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h5a.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h5b.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h5c.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Vui một chút ! Khối lập phương ở hình 6 được tạo thành từ hai miếng gỗ được ghép khít vào nhau, miếng trên và miếng dưới. (ta không nhìn thấy hai mặt bên phía sau, nhưng chúng cũng hoàn toàn giống như hai mặt trông thấy). Em hãy chỉ ra cách chế tạo khối lập phương như vậy. 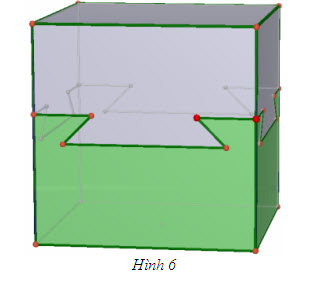
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_ch1_h6.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Câu hỏi và bài tập 1. Chứng minh rằng nếu khối đa diện có các mặt là tam giác thì số mặt phải là số chẵn. Hãy chỉ ra những khối đa diện như thế với số mặt bằng 4, 6, 8, 10. 2. Chứng minh rằng nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số chẵn. 3. Chứng minh rằng nếu khối đa diện có các mặt là tam giác và mỗi đỉnh là đỉnh chung của ba cạnh thì đó là khối tứ diện. 4. Hãy phân chia một khối hộp thành năm khối tứ diện. 5. Hãy phân chia một khối tứ diện thành bốn khối tứ diện bởi hai mặt phẳng.
School@net
|

 Xem giỏ hàng
Xem giỏ hàng


 1.
1.
 2 (h.4)
2 (h.4)




