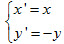| Cong ty Cong Nghe Tin hoc Nha truong | http://www.schoolnet.vn |
| Toán 11- Nâng Cao - Bài 3. Phép đối xứng trục 28/10/2011 Bài 3. Phép đối xứng trục 1. Định nghĩa phép đối xứng trục
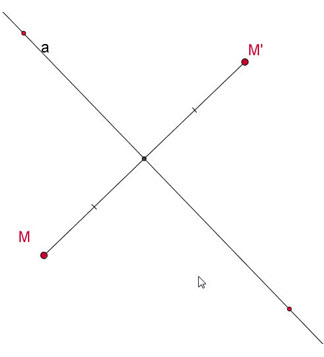
Hình 6 Tải trực tiếp tệp hình học động: L11_nc_Ch1_h6.ggb Xem trực tiếp hình vẽ động trên màn hình. Phép đối xứng qua đường thẳng a được định nghĩa như sau ĐỊNH NGHĨA 1 Phép đối xứng qua đường thẳng a là phép biến hình biến mỗi điểm M thành điểm M’ đối xứng với M qua a. Kí hiệu và thuật ngữ Phép đối xứng qua đường thẳng a thường được kí hiệu là Đa. Phép đối xứng qua đường thẳng còn gọi đơn giản là phép đối xứng trục. Đường thẳng a gọi là trục của phép đối xứng, hay đơn giản là trục đối xứng.
2. Định lí
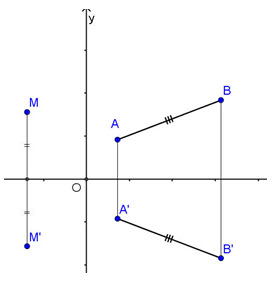
Giả sửĐa là phép đối xứng qua đường thẳng a. Ta chọn hệ trục tọa độ Oxy mà Ox là đường thẳng a (h.7).
Tải trực tiếp tệp hình học động: L11_nc_Ch1_h7.ggb Xem trực tiếp hình vẽ động trên màn hình. CHÚ Ý Qua hoạt động trên, ta thấy nếu phép đối xứng qua trục Ox biến điểm M(x ; y) thành điểm M’(x’ ; y’) thì:
Công thức trên gọi là biểu thức tọa độ của phép đối xứng qua trục Ox.
3. Trục đối xứng của một hình Chúng ta hãy quan sát bốn hình sau đây (mỗi chữ cái là một hình): A D P Q Người ta nói hình thứ nhất và hình thứ hai có tính “cân xứng” vì với mỗi hình, có thể tìm thấy một đường thẳng sao cho phép đối xứng qua đường thẳng đó biến hình ấy thành chính nó. Các đường thẳng đó gọi là trục đối xứng của mỗi hình. Hai hình còn lại không “cân xứng” vì chúng không có những đường thẳng như vậy. ĐỊNH NGHĨA 2 Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục Đd biến H thành chính nó, tức là Đd ( H ) = H. Một hình có thể không có trục đối xứng, cũng có thể có một hay nhiều trục đối xứng.
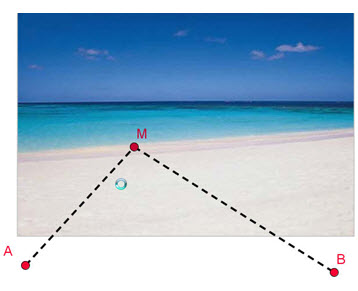
A B C D Đ E G H I K L M N O P Q R S T U V X Y Z Hãy làm thử! Các em hãy nhỏ một giọt mực lên một tờ giấy trắng, rồi gấp tờ giấy theo một đường thẳng đi qua giọt mực đó. Áp hai phần của tờ giấy sát vào nhau rồi mở ra. Các em sẽ được những hình có trục đối xứng khá kì thú! Người ta tổ chức một cuộc chạy thi trên bãi biển với điều kiện sau: Các vận động viên xuất phát từ địa điểm A và đích là địa điểm B, nhưng trước khi đến B phải nhúng mình vào nước biển (ta giả sử rằng mép nước biển là một đường thẳng) (h.8).
Tải trực tiếp tệp hình học động: L11_nc_Ch1_h8.ggb Xem trực tiếp hình vẽ động trên màn hình. Để chiến thắng trong cuộc chạy đua này, ngoài tốc độ chạy, còn có một yếu tố quan trọng là vận động viên phải xác định vị trí M ở mép nước mà mình phải chạy từ A tới để nhúng mình vào nước biển, rồi từ đó chạy đến B sao cho quãng đường phải chạy là ngắn nhất. Như vậy, bài toán có thể phát biểu dưới dạng toán học thuần túy sau đây Cho hai điểm A và B nằm về một phía của đường thẳng d (h.9). Hãy xác định điểm M trên d sao cho AM + MB bé nhất.
Tải trực tiếp tệp hình học động: L11_nc_Ch1_h9.ggb Xem trực tiếp hình vẽ động trên màn hình.
Bây giờ xét trường hợp A, B nằm về một phía của d. Hãy lấy điểm A’ đối xứng với A qua d, và chú ý rằng: AM + MB = A’M + MB.
Câu hỏi và bài tập 7. Qua phép đối xứng trục Đd (a là trục đối xứng), đường thẳng d biến thành đường thẳng d’. Hãy trả lời các câu hỏi sau: a) Khi nào thì d song song với d’ ? b) Khi nào thì d trùng với d’ ? c) Khi nào thì d cắt d’ ? Giao điểm của d và d’ có tính chất gì? d) Khi nào d vuông góc với d’ ? 8. Trong mặt phẳng tọa độ Oxy, cho các đường tròn (C1) và (C2) lần lượt có phương trình: 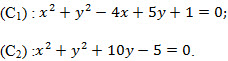 Viết phương trình ảnh của mỗi đường tròn trên qua phép đối xứng có trục Oy. 9. Cho góc nhọn xOy và một điểm A nằm trong góc đó. Hãy xác định điểm B trên Ox và điểm C trên Oy sao cho tam giác ABC có chu vi nhỏ nhất. 10. Cho hai điểm B, C cố định nằm trên đường tròn (O ; R) và điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng trục để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định. Hướng dẫn. 11. a) Chỉ ra trục đối xứng (nếu có) của mỗi hình sau đây (mỗi hình là một từ bao gồm một số chữ cái): MÂM, HOC, NHANH, HE, SHE, COACH, IS, IT, SOS, CHEO |
| URL của bài viết này::http://www.schoolnet.vn/modules.php?name=Sanpham&file=article&sid=5706 |
| © Cong ty Cong Nghe Tin hoc Nha truong | contact: sales@schoolnet.vn |
 Qua phép đối xứng trục
Qua phép đối xứng trục  1.
1.