| Cong ty Cong Nghe Tin hoc Nha truong | http://www.schoolnet.vn |
| BÍ MẬT CỦA PHẦN MỀM HÌNH HỌC ĐỘNG - BÀI 2 : CƠ SỞ TOÁN CỦA PHÉP DỰNG HYPERBOL 24/03/2008
Từ định nghĩa này, ta có một số kết quả khác mà nhiều sách coi như là định nghĩa chính thức: “Quỹ tích những điểm mà hiệu số khoảng cách tới hai điểm cố định F, F’ bằng một hằng số là một hyperbol mà hai tiêu điểm là F, F’.” Xét bài toán:
Giải Thay y = b vào phương trình của (H):
Do đó toạ độ hình chiếu K của M trên trục hoành là: mà Từ bài toán trên, ta suy ra cách dựng (H): Hiện hệ trục Oxy. Dựng hình chữ nhật cơ sở: Dựng hai đường chéo của hình chữ nhật cơ sở chính là hai đường tiệm cận của (H). Xác định đỉnh A(a ; 0) của (H). Phép vị tự tâm O tỉ số Đường vuông góc với trục Ox tại K cắt đường thẳng chứa hai cạnh của hình chữ nhật cơ sở Phép đối xứng trục Oy biến M, N lần lượt thành Cônic qua 5 điểm Muốn biết phương trình của (H) ta thực hiện: Ta có cách vẽ khác của hyperbol : Cho tiêu điểm F, F’. MF = r, MF’ = r’. Muốn tìm điểm trên hyperbol thì : Vẽ đường tròn (F, r). Vẽ đường tròn (F’, r’). Nếu hai vòng tròn cắt nhau ở hai điểm M, M’, đó là hai điểm của hyperbol. Điều kiện để có giao điểm là : Bạn đọc có thể mua một số sách “Vẽ kỹ thuật”, các cuốn sách dành cho sinh viên trường Bách khoa, để tìm hiểu rõ hơn về cách dựng hyperbol theo định nghĩa. Sau đây ta có một số bài tập về hyperbol : Bài toán 1: Cho một hyperbol tiêu điểm là F, F’. Từ một điểm M kẻ hai tiếp tuyến MT và MT’ tới hyperbol, các tiếp điểm trên nhánh (F) và (F’) là T và T’. Gọi F1 là điểm đối xứng của tiêu điểm F qua tiếp tuyến MT và gọi F1’ là điểm đối xứng của tiêu điểm F’ qua tiếp tuyến MT’. 1) Chứng minh ba điểm T, F1, F’ thẳng hàng, ba điểm T’, F1’, F thẳng hàng. 2) Chứng minh ) Gọi P và P’ là hình chiếu của F lên MT và MT’. Chứng minh Giải Trước tiên, tôi xin giới thiệu cách dựng hyperbol và cách dựng tiếp tuyến của nó. Hiện hệ trục Oxy. Dựng hình chữ nhật cơ sở: Dựng hai đường chéo của hình chữ nhật cơ sở chính là hai đường tiệm cận của (H). Xác định đỉnh A(a ; 0) của (H). Phép vị tự tâm O tỉ số Đường vuông góc với trục Ox tại K cắt đường thẳng chứa hai cạnh của hình chữ nhật cơ sở
Cônic qua 5 điểm Từ điểm P dựng ba cát tuyến PAB, PCD, PEF đến (H). Ta có AD cắt BC tại I ; CF cắt DE tại J ; IJ cắt (H) tại T, T’. Ta có PT, PT’ là hai tiếp tuyến cần dựng. Về cơ sở toán của cách dựng các tiếp tuyến, xin dành cho bạn đọc suy nghĩ. Một chút gợi ý là nó liên quan trực tiếp đến định lý Pascal. Quay trở lại bài toán 1, sau khi đã cung cấp cách dựng tiếp tuyến và cách dựng hyperbol. Từ đây, ta đi tới kết quả sau khi dựng là hình vẽ 2 của bài toán 1. Ta có sự kiểm chứng như hình vẽ 2. Ba điểm T, F1, F’ thẳng hàng. Ba điểm T’, F1’, F thẳng hàng. Các góc FMT và F’MT’ bằng nhau. Sau đây, là lời giải bằng phương pháp toán học : 1) Ta có tiếp tuyến MT là phân giác trong của góc FTF’ ; F1 là đối xứng của F qua MT nên MT là phân giác trong của góc FTF1. Do đó F1 ở trên TF’, ba điểm T, F1, F’ thẳng hàng. Tương tự ba điểm T’, F1’, F thẳng hàng. 2) Ta có |TF’ – TK| = 2a mà TF = TF1 suy ra F’F1 = 2a. tương tự FF1’ = 2a. Hai tam giác MF’F1 và MF1’F có MF’ = MF1’ ; MF1 = MF ; và F’F1 = FF1’ = 2a nên bằng nhau. Suy ra :
3) P và P’ nhìn MF dưới một góc vuông nên tứ giác MP’PF nội tiếp trong đường tròn đường kính MF. Ta có:
Ta kiểm chứng bằng phần mềm tin học học Cabri, kết quả PM = NQ như hình 3. Sau đây là cách giải bằng phương pháp toán học. Cách giải như sau : Gọi N(x1, y1) và
Giả sử (2) có nghiệm t3, t4. ta có :
Vì phương trình (1) và (2) có hệ số của t2 và hệ số của t là như nhau nên Sau đây là một số bài tập dành cho bạn đọc dựng hình, kiểm chứng và tìm quỹ tích trên phần mềm hình học động : Bài toán 3 Cho N là một điểm di động trên nhánh (F) của hyperbol có O là tâm và F là một tiêu điểm. Gọi D là tiếp tuyến với hyperbol tại N. Từ F kẻ đường vuông góc với D , cắt ON tại M. Tìm quỹ tích của M. Trên mặt phẳng toạ độ với hệ trục vuông góc Oxy, hyperbol có phương trình Vector chỉ phương của nó là
Thay (4) vào (3), ta có :
Vậy quỹ tích của M là đường chuẩn của hyperbol ứng với tiêu điểm F. Bài toán 4 Tiếp tuyến tại M của một hyperbol cắt trục ảo tại P. Gọi Q và Q’ là hình chiếu của P trên các đường thẳng MF và MF’ (F, F’ là tiêu điểm của hyperbol). a) So sánh QF và Q’F’. b) Chứng minh đường thẳng QQ’ luôn đi qua một điểm cố định khi M chạy trên hyperbol. Ta giải như sau : a) MP là phân giác trong của góc FMF’ nên PQ = PQ’. Lại có : PF = PF’. Suy ra hai tam giác vuông PQF và PQ’F’ bằng nhau. Do đó : QF = Q’F’. b) Từ F’ kẻ đường thẳng song song với MQ cắt QQ’ tại E. Ta có : Lại có QE // EF’ nên tứ giác FQF’E là hình bình hành, các đường chéo cắt nhau tại trung điểm của mỗi đường nên QQ’ luôn đi qua O. Chúng ta đã hoàn thành toàn bộ bài viết của hyperbol. Bài tiếp theo sẽ là parabol. Nó cũng chính là một trong ba thiết diện cônic. Nội dung của nó ra sao ? Xin mời các bạn đón đọc bài 3 sẽ rõ. ( Nguyễn Ngọc Giang - 229/85 - Thích Quảng Đức - |
| URL của bài viết này::http://www.schoolnet.vn/modules.php?name=News&file=article&sid=1909 |
| © Cong ty Cong Nghe Tin hoc Nha truong | contact: sales@schoolnet.vn |
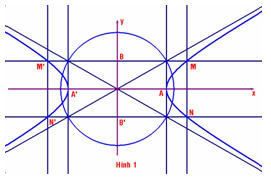 Chúng ta đã làm việc với cơ sở toán của elip. Bài viết này xin được tiếp tục giới thiệu với các bạn cơ sở toán của phép dựng hyperbol. Cũng như elip, hyperbol là conic có tâm. Một số định nghĩa như sau : “Hyperbol là quỹ tích tâm các đường tròn tiếp xúc với một đường tròn cố định (F’) và đi qua một điểm F ở ngoài đường tròn đó. F và F’ gọi là tiêu điểm”.
Chúng ta đã làm việc với cơ sở toán của elip. Bài viết này xin được tiếp tục giới thiệu với các bạn cơ sở toán của phép dựng hyperbol. Cũng như elip, hyperbol là conic có tâm. Một số định nghĩa như sau : “Hyperbol là quỹ tích tâm các đường tròn tiếp xúc với một đường tròn cố định (F’) và đi qua một điểm F ở ngoài đường tròn đó. F và F’ gọi là tiêu điểm”.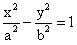 . Gọi M là điểm trên (H) có tung độ bằng b và có hoành độ dương. Gọi K là hình chiếu của M trên trục Ox và A là đỉnh có hoành độ dương của (H).
Hãy tính tỉ số
. Gọi M là điểm trên (H) có tung độ bằng b và có hoành độ dương. Gọi K là hình chiếu của M trên trục Ox và A là đỉnh có hoành độ dương của (H).
Hãy tính tỉ số 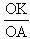 .
.
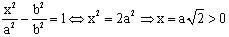
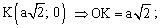
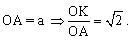
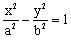 trong mặt phẳng Oxy theo 5 điểm như sau:
trong mặt phẳng Oxy theo 5 điểm như sau: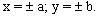 .
.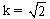 , biến điểm A thành điểm K.
, biến điểm A thành điểm K.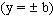 tại M và N.
tại M và N.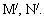 .
.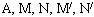 là hyperbol cần dựng.
là hyperbol cần dựng. 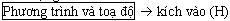 , khi đó ta có ngay phương trình của (H).
, khi đó ta có ngay phương trình của (H).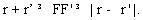
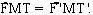
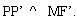
 Phép đối xứng trục Oy biến M, N lần lượt thành
Phép đối xứng trục Oy biến M, N lần lượt thành 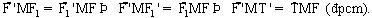
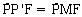 (góc nội tiếp). mà
(góc nội tiếp). mà 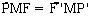 nên
nên 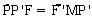 . Lại có
. Lại có 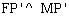 . Do đó
. Do đó 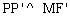 (đpcm).
(đpcm).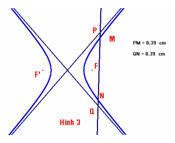 Bài toán 2 Cho hyperbol (H) :
Bài toán 2 Cho hyperbol (H) : 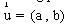 lần lượt là một điểm của d và vector chỉ phương của đường thẳng đó. Phương trình tham số của đường thẳng d là : x = x1 + at ; y = y1 + bt Giao điểm M, N có toạ độ là nghiệm của hệ :
lần lượt là một điểm của d và vector chỉ phương của đường thẳng đó. Phương trình tham số của đường thẳng d là : x = x1 + at ; y = y1 + bt Giao điểm M, N có toạ độ là nghiệm của hệ : 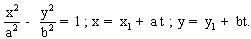 Ta được
Ta được 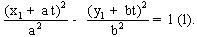 . Giả sử (1) có nghiệm t1, t2. Ta có :
. Giả sử (1) có nghiệm t1, t2. Ta có : 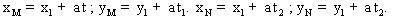 Giao điểm P, Q là nghiệm của hệ :
Giao điểm P, Q là nghiệm của hệ :
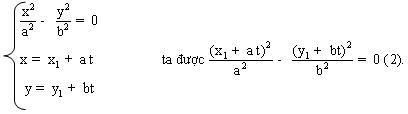
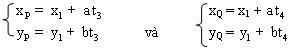
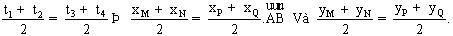 Do đó, trung điểm của MN và trung điểm của PQ trùng nhau. Nghĩa là : PM = NQ.
Do đó, trung điểm của MN và trung điểm của PQ trùng nhau. Nghĩa là : PM = NQ.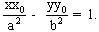
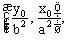 vậy phương trình của đường thẳng qua F(c, 0) và vuông góc với d là :
vậy phương trình của đường thẳng qua F(c, 0) và vuông góc với d là : 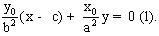 Đường thẳng ON có phương trình
Đường thẳng ON có phương trình 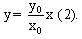 Vậy toạ độ (x, y) của điểm M là nghiệm của hệ phương trình :
Vậy toạ độ (x, y) của điểm M là nghiệm của hệ phương trình :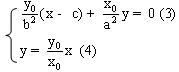
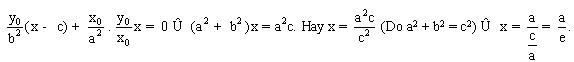
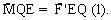 Ta lại có :
Ta lại có : 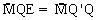 (vì tam giác MQQ’ cân tại đỉnh M và
(vì tam giác MQQ’ cân tại đỉnh M và 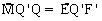 (đối đỉnh), suy ra :
(đối đỉnh), suy ra : 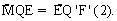 Từ (1) và (2) :
Từ (1) và (2) : 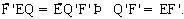 Suy ra QF = EF’.
Suy ra QF = EF’.