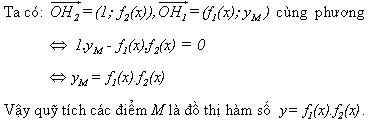Ta biết rằng từ đồ thị hàm số (C): y = f(x) ta có thể vẽ đồ thị hàm số (C1): y = f(|x|); (C2): y =|f(x)|, (C3): y = -f(x), (C4): y = f(-x), (C5): y = f-1(x) (nếu hàm số f có hàm số ngược trên khoảng xác định của nó), (C6): y = - f(-x), (C7): y = f(x + a), (C8): y = f(x) + b, bằng các phép đối xứng trục, phép đối xứng tâm, phép tịnh tiến phù hợp.
Vấn đề được đặt ra là: khi đã cho biết những đồ thị hàm số y = f1(x), y = f2(x), y = f(x) thì ta có thể vẽ các đồ thị hàm số có dạng y = k1.f1(x) + k2.f2(x) (k1, k2 là hai số thực khác không), 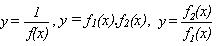 hay không? và cách vẽ như thế nào? Câu trả lời là được bài viết sẽ giải quyết trọn vẹn vấn đề đó.
hay không? và cách vẽ như thế nào? Câu trả lời là được bài viết sẽ giải quyết trọn vẹn vấn đề đó.
1. Cách vẽ đồ thị hàm số y = k1.f1(x) + k2.f2(x) khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x) (k1, k2 là hai số thực khác không)
1.1. Bài toán I
Trong mặt phẳng với hệ toạ độ Oxy cho hai đồ thị (C1) : y = f1(x), (C2) : y = f2(x) và ba đường thẳng (d1): x = 2k1, (d2) : x = 2k2, (d3): x = 1 (k1.k2 ≠ ). Lấy điểm M1 trên đồ thị (C1) sao cho đường thẳng (d) qua M1 vuông góc với x’Ox cắt đồ thị (C2) tại điểm M2. Gọi H1 là hình chiếu vuông góc của M1 lên đường thẳng (d3), đường thẳng OH1 cắt đường thẳng (d1) tại P1, gọi Q1 là hình chiếu vuông góc của điểm P1 lên đường thẳng (d). Gọi H2 là hình chiếu vuông góc của điểm M2 lên đường thẳng (d3), đường thẳng OH2 cắt đường thẳng (d2) tại P2 , gọi Q2 là hình chiếu vuông góc của điểm P2 lên đường thẳng (d).
Tìm quỹ tích các trung điểm M của đoạn Q1Q2 khi M1 chạy trên đồ thị (C1).
Lời giải:
Giả sử M(x; yM ) với x ∈ D1 ∩ D2 trong đó D1 và D2 là hai tập xác định của hai hàm số f1(x) và f2(x), từ giả thiết ta có H(x; 0), M1(x; f1(x)), M2(x; f2(x)), H1(1; f1(x)), H2(1; f2(x)),
P1(2k1; y1), P2(2k2; y2), Q1(x; y1), Q2(x; y2). Ta có:
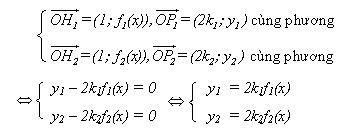
Vì M là trung điểm của đoạn Q1Q2 nên 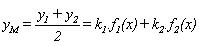
Vậy quỹ tích các điểm M là đồ thị hàm số y = k1.f1(x) + k2.f2(x).
(ở đây tôi không trình bày chứng minh phần đảo)
1.2. Thuật toán vẽ đồ thị hàm số y = k1.f1(x) + k2.f2(x) khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x) (k1, k2 là hai số thực khác không)
B1 : Vẽ đồ thị hàm số (C1): y = f1(x), (C2): y = f2(x).
B2 : Vẽ ba đường thẳng (d1): x = 2k1, (d2): x = 2k2, (d3): x = 1
B3 : Lấy điểm M1 ∈ (C1), qua M1 ta vẽ đường thẳng (d) vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2
B4 : + Dựng điểm H1 là hình chiếu vuông góc của điểm M1 lên đường thẳng (d3 ). Lấy giao điểm P1 của đường thẳng OH1 và đường thẳng (d1).
+ Dựng Q1 là hình chiếu vuông góc của điểm P1 lên đường thẳng (d).
+ Dựng điểm H2 là hình chiếu vuông góc của điểm M2 lên đường thẳng (d3 ). Lấy giao điểm P2 của đường thẳng OH2 và đường thẳng (d2).
+ Dựng Q2 là hình chiếu vuông góc của điểm P2 lên đường thẳng (d).
B5: Dựng trung điểm M của đoạn Q1Q2.
Khi đó ta cho M1 chạy trên đồ thị (C1) thì điểm M vạch nên đồ thị hàm số y = k1.f1(x) + k2.f2(x) (k1, k2 là hai số thực khác không).
Ví dụ 1
Từ đồ thị hai hàm số y = x3 và y = x2 hãy vẽ đồ thị hàm số y = 2x3 - 3x2 bằng phần
mềm hình học The Geometer’s Sketchpad.
B1: Vẽ đồ thị hàm số (C1): y =x2, (C2): y = x3 (thực hiện lệnh Graph / Plot New Fulction …)
B2 : Vẽ ba đường thẳng (d1): x = 4, (d2): x = -6, (d3): x = 1 (thực hiện lệnh Plot Points… để xác định ba điểm có toạ độ Ă4;0), B(-6;0), C(1;0); để vẽ đường thẳng (d1) ta chọn điểm A và chọn trục hoành Ox rồi thực hiện lệnh Construct / Perpendicular Line; để vẽ đường thẳng (d2) ta chọn điểm B và chọn trục hoành Ox, sau đó thực hiện lệnh Construct / Perpendicular Line; để vẽ đường thẳng (d3) ta chọn điểm C và chọn trục hoành Ox, sau đó thực hiện lệnh Construct / Perpendicular Line).
B3: Lấy điểm M1 ∈ (C1), qua M1 ta vẽ đường thẳng (d) vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2 (chọn M1, chọn trục hoành Ox, thực hiện lệnh Construct / Perpendicular Line).
B4 : + Dựng điểm H1 là hình chiếu vuông góc của điểm M1 lên đường thẳng (d3 ). Lấy giao điểm P1 của đường thẳng OH1 và đường thẳng (d1) (chọn điểm M1, chọn đường thẳng (d3), thực hiện lệnh Construct / Perpendicular Line; chọn hai điểm O, H1 rồi thực hiện lệnh Construct / Line)
+ Dựng Q1 là hình chiếu vuông góc của điểm P1 lên đường thẳng (d)( chọn điểm P1, chọn đường thẳng (d), thực hiện lệnh Construct / Perpendicular Line ).
+ Dựng điểm H2 là hình chiếu vuông góc của điểm M2 lên đường thẳng (d3 ). Lấy giao điểm P2 của đường thẳng OH2 và đường thẳng (d2) (chọn điểm M2, chọn đường thẳng (d3), thực hiện lệnh Construct / Perpendicular Line; chọn hai điểm O, H2 rồi thực hiện lệnh Construct / Line).
+ Dựng Q2 là hình chiếu vuông góc của P2 lên đường thẳng (d); chọn điểm P2, chọn đường thẳng (d), thực hiện lệnh Construct / Perpendicular Line ).
B5: Dựng trung điểm M của đoạn Q1Q2 (chọn đoạn thẳng Q1Q2, thực hiện lệnh Construct / Midpoint)
B6: Chọn điểm M, tạo vết chọn màu ( thực hiện lệnh Display / Trace Point / Color)
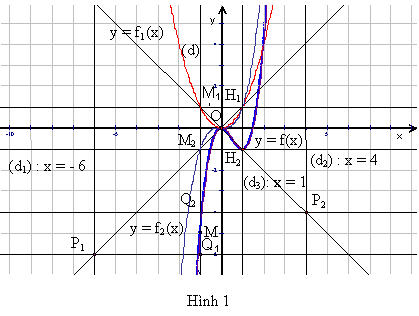
B7: Chọn điểm M1, thực hiện lệnh Display / Animate Point thì điểm M đã được tô màu vạch nên đồ thị (C’ ) : y = 2x3 - 3x2 (xem hình 1).
2. Cách vẽ đồ thị hàm số 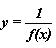 khi cho biết đồ thị hàm số y = f(x)
khi cho biết đồ thị hàm số y = f(x)
2.1. Bài toán II
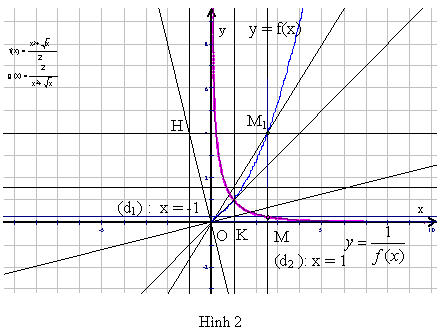
Trong mặt phẳng với hệ toạ độ Oxy cho đồ thị (C): y = f(x) và hai đường thẳng (d1) : x = - 1, (d2) : x = 1. Vẽ đường thẳng (d) vuông góc với x’Ox sao cho cắt đồ thị (C) tại M1. Gọi H là hình chiếu vuông góc của M1 lên đường thẳng (d1). Đường thẳng qua O vuông góc với OH cắt đường thẳng (d2) tại K. Gọi M là hình chiếu vuông góc của điểm K lên đường thẳng (d).
Tìm quỹ tích các điểm M khi M1 chạy trên đồ thị (C).
Lời giải
Giả sử M(x; yM) thì M1(x; f(x)), với x thuộc tập xác định của hàm số f(x), từ giả thiết ta có H(-1; f(x)), K(1; yM). Ta có:
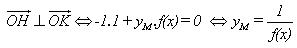
Vậy quỹ tích các điểm M là đồ thị hàm số 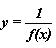
2.2.Thuật toán vẽ đồ thị hàm 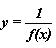 khi cho biết đồ thị hàm số y = f(x)
khi cho biết đồ thị hàm số y = f(x)
B1 : Vẽ đồ thị hàm số (C): y = f(x)
B2 : Vẽ hai đường thẳng (d1): x = -1, (d2): x = 1
B3 : Lấy điểm M1 ∈ (C) , qua M1 ta vẽ đường thẳng (d) vuông góc với trục hoành Ox
B4 : Dựng điểm H là hình chiếu vuông góc của M1 lên đường thẳng (d1 ).
B5 : Dựng đường thẳng qua O vuông góc với OH cắt đường thẳng (d2) tại K.
B6 : Dựng điểm M là hình chiếu vuông góc của điểm K lên đường thẳng (d).
Khi đó ta cho M1 chạy trên đồ thị (C) thì điểm M vạch nên đồ thị hàm số 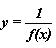
Ví dụ 2: Từ đồ thị hàm số 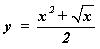 hãy vẽ đồ thị hàm số
hãy vẽ đồ thị hàm số 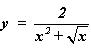 bằng phần mềm hình học The Geometer’s Sketchpad.
bằng phần mềm hình học The Geometer’s Sketchpad.
B1 : Vẽ đồ thị hàm số (C): y = f(x) (thực hiện lệnh Graph / Plot New Fulction …)
B2 : Vẽ hai đường thẳng (d1): x = -1, (d2): x = 1 (thực hiện lệnh Plot Points… để xác định hai điểm có toạ độ ; để vẽ đường thẳng (d1) ta chọn điểm A và chọn trục hoành Ox rồi thực hiện lệnh Construct / Perpendicular Line; để vẽ đường thẳng (d2) ta chọn điểm B và chọn trục hoành sau đó thực hiện lệnh Construct / Perpendicular Line).
B3 : Lấy điểm M1 ∈ (C), qua M1 ta vẽ đường thẳng (d) vuông góc với trục hoành Ox (chọn M1, chọn trục hoành Ox, thực hiện lệnh Construct / Perpendicular Line).
B4 : Dựng điểm H là hình chiếu vuông góc của M1 lên đường thẳng (d1 ) (chọn điểm M1, chọn đường thẳng (d1), thực hiện lệnh Construct / Perpendicular Line).
B5 : Dựng đường thẳng qua O vuông góc với OH, xác định giao điểm K của đường này với đường thẳng (d2)(chọn điểm O, chọn đường thẳng OH, thực hiện lệnh Construct / Perpendicular Line).
B6 : Dựng điểm M là hình chiếu vuông góc của điểm K lên đường thẳng (d) (chọn điểm K, chọn đường thẳng (d), thực hiện lệnh Construct / Perpendicular Line).
B7 : Chọn điểm M, tạo vết chọn màu (Thực hiện lệnh Display / Trace Point / Color)
B8 : Chọn điểm M1, thực hiện lệnh Display / Animate Point thì điểm M đã được tô màu vạch nên đồ thị (C’’) : 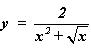 (xem hình 2).
(xem hình 2).
3. Cách vẽ đồ thị hàm số y = f1(x).f2(x) khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x)
3.1.Bài toán III
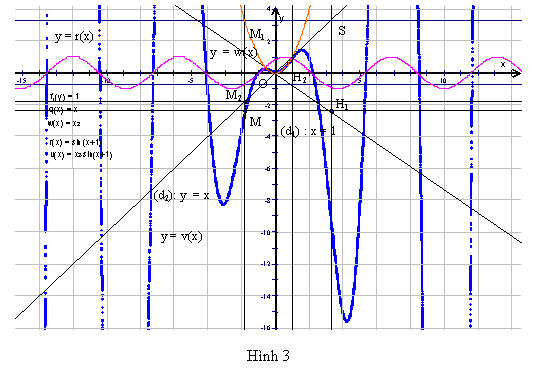
Trong mặt phẳng với hệ toạ độ Oxy cho hai đồ thị (C1): y = f1(x), (C2): y = f2(x) và hai đường thẳng (d1): x = 1, (d2) : y = x. Lấy điểm M1 trên đồ thị (C1) sao cho đường thẳng (d) qua M1 vuông góc với x’Ox cắt đồ thị (C2) tại điểm M2. Gọi H2 là hình chiếu vuông góc của M2 lên đường thẳng (d1), đường thẳng qua M1 vuông góc với Oy cắt đường thẳng (d2) tại S,
đường thẳng qua S vuông góc với x’Ox cắt đường thẳng OH2 tại H1. Gọi M là hình chiếu vuông góc của điểm H1 lên đường thẳng (d).
Tìm quỹ tích các điểm M khi điểm M1 chạy trên đồ thị (C1).
Lời giải
Giả sử M(x; yM) với x ∈ D1 ∩ D2 trong đó D1 và D2 là hai tập xác định của hai hàm số f1(x) và f2(x), từ giả thiết ta có M1(x; f1(x)), S(f1(x); f1(x)) M2(x; f2(x)), H2(1; f2(x)), H1(f1(x); yM).
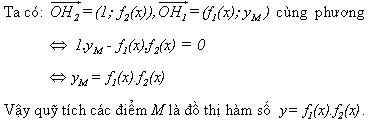

 Xem giỏ hàng
Xem giỏ hàng Sử dụng phần mềm này, các bạn có thể thực hiện được nhiều bài toán hình học phục vụ giảng dạy.
Sử dụng phần mềm này, các bạn có thể thực hiện được nhiều bài toán hình học phục vụ giảng dạy.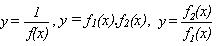 hay không? và cách vẽ như thế nào? Câu trả lời là được bài viết sẽ giải quyết trọn vẹn vấn đề đó.
hay không? và cách vẽ như thế nào? Câu trả lời là được bài viết sẽ giải quyết trọn vẹn vấn đề đó.
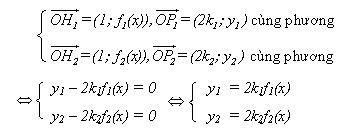

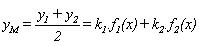
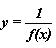 khi cho biết đồ thị hàm số y = f(x)
khi cho biết đồ thị hàm số y = f(x) 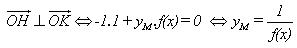

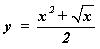 hãy vẽ đồ thị hàm số
hãy vẽ đồ thị hàm số 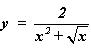 bằng phần mềm hình học The Geometer’s Sketchpad.
bằng phần mềm hình học The Geometer’s Sketchpad.