Ngày gửi bài: 12/04/2007
Số lượt đọc: 6436
|
Các bạn có thể tải phần mềm AGL bản DEMO tại đây.
Mặc dù phần mềm cung cấp cho các thầy giáo, cô giáo các công cụ liên quan đến các bài giảng đó, nhưng vấn đề áp dụng nó như thế nào vào bài giảng của các thầy giáo, cô giáo còn phụ thuộc rất nhiều vào ý tưởng khai thác và truyền đạt của các thầy giáo, cô giáo đối với bài đó. Trong bài viết này tôi muốn đưa ra một cách riêng của mình trong ý tưởng dạy các bài lượng giác có sử dụng phần mềm AGL. Ý tưởng này có được khi tôi thiết kế phần mềm.
Trước tiên tôi liệt kê những công cụ mà phần mềm AGL cung cấp cho các thầy giáo, cô giáo khi giảng về các bài lượng giác.
* Cung có số đo 1rad
* Tương ứng số thực với một điểm trên đường tròn lượng giác.
* Góc và cung lượng giác.
* Giá trị lượng giác.
* Ý nghĩa hình học của tan và cot
* Cung – góc bù nhau.
* Cung – góc đối nhau.
* Cung – góc phụ nhau.
* Cung – góc hơn kém nhau Π.
1. Dùng phần mềm AGL minh hoạ cung có số đo 1rad
Đầu tiên bạn khởi động phần mềm AGL, sau khi cài đặt có biểu tượng  trên màn hình. Bạn chọn mục Đại số -> Lớp 10 -> Lượng giác (bấm vào các dấu cộng trước mỗi mục). Cuối cùng bạn chọn mục trên màn hình. Bạn chọn mục Đại số -> Lớp 10 -> Lượng giác (bấm vào các dấu cộng trước mỗi mục). Cuối cùng bạn chọn mục  thì màn hình sẽ hiện ra như sau: thì màn hình sẽ hiện ra như sau:
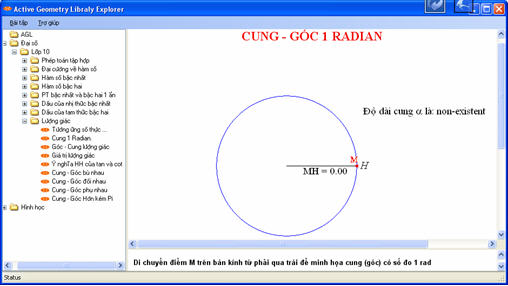
Nếu chưa thấy xuất hiện phần trợ giúp ở phía dưới cửa số ta bấm vào menu “Trợ giúp” của phần mềm. 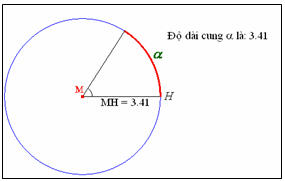 Ban đầu các ta thấy dòng chữ “Độ dài cung α là: non – existent”, chữ non – existent có nghĩa là không tồn tại (tiếng Pháp).
Ban đầu các ta thấy dòng chữ “Độ dài cung α là: non – existent”, chữ non – existent có nghĩa là không tồn tại (tiếng Pháp).
Để minh hoạ cho học sinh thấy được độ dài của cung có số đo 1rad bằng bán kính của đường tròn, ta di chuyển điểm M từ phải qua trái trên bán kính, khi đó có một cung màu đỏ xuất hiện với độ dài của cung đó bằng độ dài đoạn MH. Khi M trùng tâm đường tròn thì cung màu đỏ sẽ có số đo 1rad. Như hình bên.
2. Dùng phần mềm AGL minh hoạ tương ứng mỗi số thực với một điểm trên đường tròn lượng giác
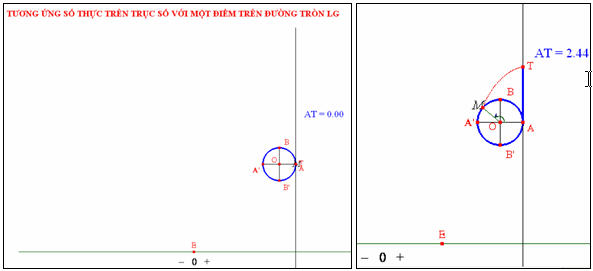
Ta chọn mục “Tương ứng số thực…” thì màn hình sẽ hiện ra như hình dưới đây.
Để minh hoạ với mỗi điểm T trên trục sẽ có một điểm M trên đường tròn lượng giác ứng với nó dựa vào độ dài đại số của đoạn AT trên trục và số đo của cung lượng giác AM trên đường tròn lượng giác, ta di chuyển điểm E trên thanh trượt thì điểm T sẽ di chuyển trên trục và điểm M di chuyển trên đường tròn lượng giác. Trên hình vẽ lúc này có một đường “- - - ” nối điểm T với điểm M để giúp ta giải thích với học sinh sự tương ứng đó (đường Xiclôit) hình dưới. Để cụ thể hơn ta nên di chuyển để cung lượng giác AM lần lượt có số đo Π/2, Π, -Π/2, và -Π từ đó lần lượt so sánh với độ dài đại số của đoạn AT trên trục. Ví dụ M trùng B hì cung lượng giác AM có số đo là Π/2, khi đó độ dài đại số đoạn AT trên rục là 1,57.
3. Dùng phần mềm AGL minh hoạ góc và cung lượng giác
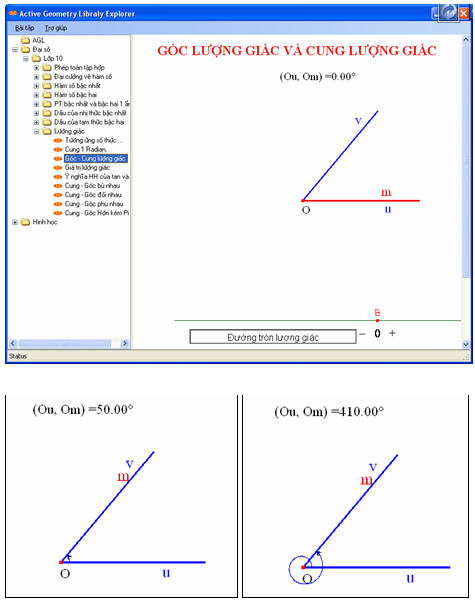
Ta chọn mục “Góc – Cung lượng giác” thì màn hình sẽ hiện ra như hình dưới.
Để minh hoạ góc lượng giác, ta di chuyển điểm E trên thanh trượt, khi đó tia Om sẽ di chuyển theo chiều dương hay chiều âm tuỳ theo ta di chuyển điểm E sang bên dấu (+) hay bên dấu (-). Nếu Om trùng với Ov thì tia Om quét được góc lượng giác (Ou, Ov). Với phần minh hoạ này ta dễ dàng minh hoạ cho học sinh những góc lượng giác khác nhau nhưng đều có tia đầu là Ou và tia cuối là Ov.
Để minh hoạ cung lượng giác, ta di chuyển điểm E trên thanh trượt về vị trí 0, sau đó bấm nút thì đường tròn lượng giác hiện ra. Ban di chuyển điểm E trên thanh trượt thì điểm M là giao của tia Om và đường ròn sẽ vạch rên đường tròn một cung lượng giác α. Xem hình dưới. thì đường tròn lượng giác hiện ra. Ban di chuyển điểm E trên thanh trượt thì điểm M là giao của tia Om và đường ròn sẽ vạch rên đường tròn một cung lượng giác α. Xem hình dưới.
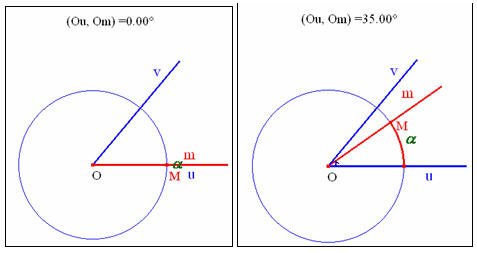
Khi sử dụng minh hoạ này ta cũng dễ dàng đồng nhất số đo của góc lượng giác (Ou, Om) với số đo của cung α.
4. Dùng phần mềm AGL minh hoạ giá trị lượng giác
Ta chọn mục “Giá trị lượng giác” thì màn hình sẽ hiện ra như hình dưới.
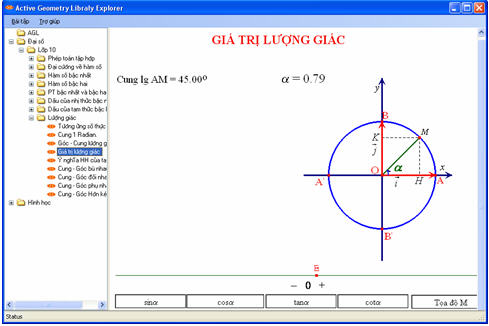
Trên màn hình có dãy nút bấm  để ta lần lượt cho xuất hiện định nghĩa các giá trị lượng giác. Để thay đổi cung lượng giác AM ta di chuyển E trên thanh trượt.
Để khắc sâu định nghĩa các giá trị lượng giác, ta cho thay đổi cung lượng giác, trên màn hình sẽ có ố đo của cung lượng giác đó, sau đó ta bấm nút để ta lần lượt cho xuất hiện định nghĩa các giá trị lượng giác. Để thay đổi cung lượng giác AM ta di chuyển E trên thanh trượt.
Để khắc sâu định nghĩa các giá trị lượng giác, ta cho thay đổi cung lượng giác, trên màn hình sẽ có ố đo của cung lượng giác đó, sau đó ta bấm nút  để xuất hiện tọa độ điểm M, từ đó yêu cầu học sinh cho biết sin và cos của cung lượng giác AM tương ứng.
5. Dùng phần mềm AGL minh hoạ ý nghĩa hình học của tan và cot
Ta chọn mục “Ý nghĩa HH của tan và cot” .
Trên màn hình sẽ có phần điều khiển như hình dưới đây: để xuất hiện tọa độ điểm M, từ đó yêu cầu học sinh cho biết sin và cos của cung lượng giác AM tương ứng.
5. Dùng phần mềm AGL minh hoạ ý nghĩa hình học của tan và cot
Ta chọn mục “Ý nghĩa HH của tan và cot” .
Trên màn hình sẽ có phần điều khiển như hình dưới đây:

Để nói nên ý nghĩa hình học của tan, bạn bấm nút “Ý nghĩa HH của tan”, khi đó màn hình sẽ như sau:
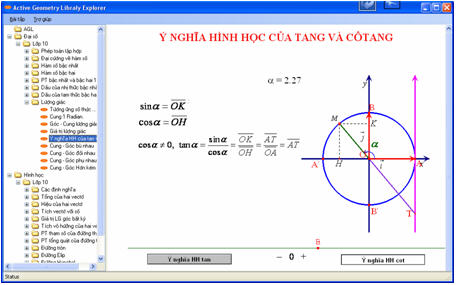
Từ đó ta cùng học sinh chứng minh được tanα = 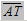 và hình thành khái niệm, cũng như ý nghĩa của trục tan.
Phần ý nghĩa hình học của cot tương tự.
6. Dùng phần mềm AGL minh hoạ giá trị lượng giác của các cung lượng giác bù nhau
Ta chọn mục “Cung – Góc bù nhau”.
Khi đó trên màn hình sẽ xuất hiện đường tròn lượng giác với hai cung lượng giác bù nhau là cung lượng giác AM và cung lượng giác AM, phía trên có số đo (rad) của hai cung đó. Để phân biệt hai cung và số đo của chúng ta chú ý đến mầu sắc của các đối ượng trên đó, những đối tượng cùng màu là tương ứng với nhau.
Di chuyển E để thấy được mối liên hệ giữa hai cung lượng giác bù nhau.
Đầu tiên ta bấm nút “Sin”, màn hình hiển thị như sau: và hình thành khái niệm, cũng như ý nghĩa của trục tan.
Phần ý nghĩa hình học của cot tương tự.
6. Dùng phần mềm AGL minh hoạ giá trị lượng giác của các cung lượng giác bù nhau
Ta chọn mục “Cung – Góc bù nhau”.
Khi đó trên màn hình sẽ xuất hiện đường tròn lượng giác với hai cung lượng giác bù nhau là cung lượng giác AM và cung lượng giác AM, phía trên có số đo (rad) của hai cung đó. Để phân biệt hai cung và số đo của chúng ta chú ý đến mầu sắc của các đối ượng trên đó, những đối tượng cùng màu là tương ứng với nhau.
Di chuyển E để thấy được mối liên hệ giữa hai cung lượng giác bù nhau.
Đầu tiên ta bấm nút “Sin”, màn hình hiển thị như sau:
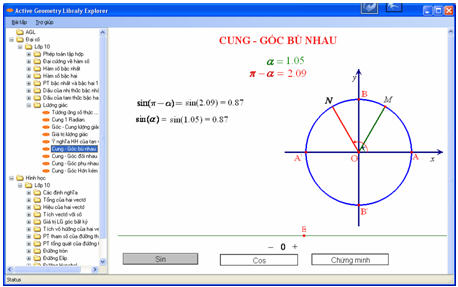
Ta di chuyển điểm E sẽ thấy giá trị của sin(Π-α) và sinα thay đổi, sau đó cho học sinh nhận xét một cách tổng quát về sin(Π-α) và sinα (Ta có thể dùng những trường hợp đặc biệt để cho học sinh so sánh trước khi cho hiện kết quả trên màn hình).
Phần cos(Π-α) và cosα ta làm tương tự.
Cuối cùng ta bấn nút “Chứng minh” để cùng học sinh chứng minh kết quả nhận định ở trên.
Phần giá trị lượng giác của các cung đối nhau, các cung phụ nhau và các cung hơn kém Pi, ta cũng làm hoàn toàn tương tự.
Thưa các bạn, những bạn đọc đến đây tôi tin chắc rằng các bạn cũng có một niềm đam mê như tôi về việc sử dụng các đối tượng hình học động để góp phần vào việc giảng dạy môn toán sao cho có hiệu quả hơn, giúp các em học sinh lĩnh hội tri thức nhanh hơn và nhớ lâu hơn. Qua đây tôi muốn bày tỏ một quan điểm mang tính cá nhân trong việc sử dụng các đối tượng hình học động để giảng dạy toán đó là: Đối với học sinh trung bình và yếu, thì việc thông qua các đối tượng hình học động, các em tự nhận thấy được những kết quả toán học kiểu như là sin(Π-α) = sinα, và cos(Π-α) = - cosα và biết vận dụng kết quả đó trong học tập đã là một sự thành công, còn đối với học sinh khá, giỏi đặc biệt là những em học sinh yêu thích toán học thì các em nên chứng minh để khẳng định tính đúng đắn của kết quả đó.
Cuối cùng, tôi rất mong các bạn quan tâm đến phần mềm thư viện hình học động AGL hãy đóng góp ý kiến cho tôi theo nhiều góc độ chuyên môn để tôi có thể tạo ra một phần mềm mang lại nhiều hiệu quả trong việc trợ giúp các thầy giáo, cô giáo giảng dạy bộ môn toán. Giúp các em học sinh của chúng ta có điều kiện khám phá và lĩnh hội tri thức dễ dàng hơn, phong phú hơn.
Dương Mạnh Trí
|

 Xem giỏ hàng
Xem giỏ hàng Dương Mạnh Trí – duongmanhtri@vnn.vn
Dương Mạnh Trí – duongmanhtri@vnn.vn trên màn hình. Bạn chọn mục Đại số -> Lớp 10 -> Lượng giác (bấm vào các dấu cộng trước mỗi mục). Cuối cùng bạn chọn mục
trên màn hình. Bạn chọn mục Đại số -> Lớp 10 -> Lượng giác (bấm vào các dấu cộng trước mỗi mục). Cuối cùng bạn chọn mục  thì màn hình sẽ hiện ra như sau:
thì màn hình sẽ hiện ra như sau:

 Ban đầu các ta thấy dòng chữ “Độ dài cung α là: non – existent”, chữ non – existent có nghĩa là không tồn tại (tiếng Pháp).
Ban đầu các ta thấy dòng chữ “Độ dài cung α là: non – existent”, chữ non – existent có nghĩa là không tồn tại (tiếng Pháp). 

 thì đường tròn lượng giác hiện ra. Ban di chuyển điểm E trên thanh trượt thì điểm M là giao của tia Om và đường ròn sẽ vạch rên đường tròn một cung lượng giác α. Xem hình dưới.
thì đường tròn lượng giác hiện ra. Ban di chuyển điểm E trên thanh trượt thì điểm M là giao của tia Om và đường ròn sẽ vạch rên đường tròn một cung lượng giác α. Xem hình dưới.

 để ta lần lượt cho xuất hiện định nghĩa các giá trị lượng giác. Để thay đổi cung lượng giác AM ta di chuyển E trên thanh trượt.
Để khắc sâu định nghĩa các giá trị lượng giác, ta cho thay đổi cung lượng giác, trên màn hình sẽ có ố đo của cung lượng giác đó, sau đó ta bấm nút
để ta lần lượt cho xuất hiện định nghĩa các giá trị lượng giác. Để thay đổi cung lượng giác AM ta di chuyển E trên thanh trượt.
Để khắc sâu định nghĩa các giá trị lượng giác, ta cho thay đổi cung lượng giác, trên màn hình sẽ có ố đo của cung lượng giác đó, sau đó ta bấm nút  để xuất hiện tọa độ điểm M, từ đó yêu cầu học sinh cho biết sin và cos của cung lượng giác AM tương ứng.
5. Dùng phần mềm AGL minh hoạ ý nghĩa hình học của tan và cot
Ta chọn mục “Ý nghĩa HH của tan và cot” .
Trên màn hình sẽ có phần điều khiển như hình dưới đây:
để xuất hiện tọa độ điểm M, từ đó yêu cầu học sinh cho biết sin và cos của cung lượng giác AM tương ứng.
5. Dùng phần mềm AGL minh hoạ ý nghĩa hình học của tan và cot
Ta chọn mục “Ý nghĩa HH của tan và cot” .
Trên màn hình sẽ có phần điều khiển như hình dưới đây:


 và hình thành khái niệm, cũng như ý nghĩa của trục tan.
Phần ý nghĩa hình học của cot tương tự.
6. Dùng phần mềm AGL minh hoạ giá trị lượng giác của các cung lượng giác bù nhau
Ta chọn mục “Cung – Góc bù nhau”.
Khi đó trên màn hình sẽ xuất hiện đường tròn lượng giác với hai cung lượng giác bù nhau là cung lượng giác AM và cung lượng giác AM, phía trên có số đo (rad) của hai cung đó. Để phân biệt hai cung và số đo của chúng ta chú ý đến mầu sắc của các đối ượng trên đó, những đối tượng cùng màu là tương ứng với nhau.
Di chuyển E để thấy được mối liên hệ giữa hai cung lượng giác bù nhau.
Đầu tiên ta bấm nút “Sin”, màn hình hiển thị như sau:
và hình thành khái niệm, cũng như ý nghĩa của trục tan.
Phần ý nghĩa hình học của cot tương tự.
6. Dùng phần mềm AGL minh hoạ giá trị lượng giác của các cung lượng giác bù nhau
Ta chọn mục “Cung – Góc bù nhau”.
Khi đó trên màn hình sẽ xuất hiện đường tròn lượng giác với hai cung lượng giác bù nhau là cung lượng giác AM và cung lượng giác AM, phía trên có số đo (rad) của hai cung đó. Để phân biệt hai cung và số đo của chúng ta chú ý đến mầu sắc của các đối ượng trên đó, những đối tượng cùng màu là tương ứng với nhau.
Di chuyển E để thấy được mối liên hệ giữa hai cung lượng giác bù nhau.
Đầu tiên ta bấm nút “Sin”, màn hình hiển thị như sau:



