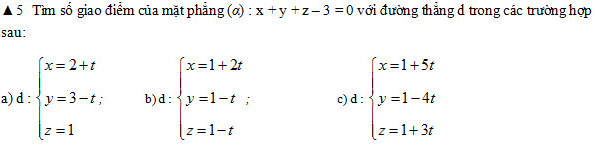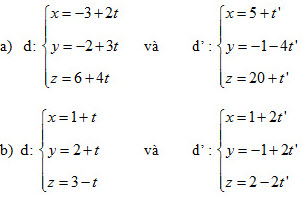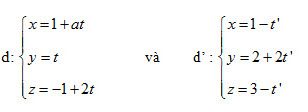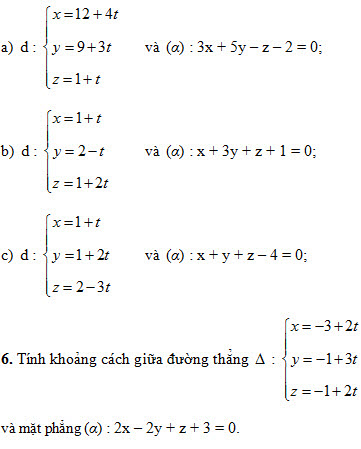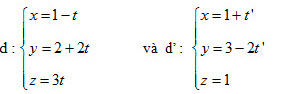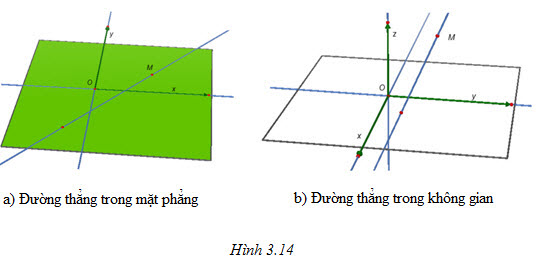
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch3_h3.14a.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch3_h3.14b.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
I – PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
1 Trong không gian Oxyz cho điểm M0(1;2;3) và gau đuển M1 (1+t ; 2+t ; 3+t), M2(1+2t ; 2+2t ; 3+2t) di động với tham số t. Hãy chứng tỏ ba điểm M0, M1, M2 luôn thẳng hàng.
Định lí
Trong không gian Oxyz cho đường thẳng 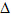 đi qua điểmM0 (x0; y0 ; z0 ) và nhận đi qua điểmM0 (x0; y0 ; z0 ) và nhận 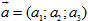 làm vecto chỉ phương. làm vecto chỉ phương. Điều kiện cần và đủ để điểm M(x ; y ; z) nằm trên 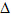 là một số thực t sao cho là một số thực t sao cho
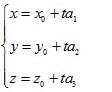
Chứng minh

Định nghĩa
Phương trình tham số của đường thẳng 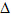 đi qua điểm M0 (x0; y0 ; z0 ) và có vecto chỉ phương đi qua điểm M0 (x0; y0 ; z0 ) và có vecto chỉ phương 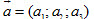 là phương trình có dạng
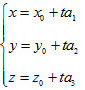
trong đó t là tham số.
Chú ý. Nếu a1;a2;a3 đều khác 0 thì người ta còn có thể viết phương trình của đường thẳng 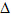 dưới dạng chính tắc như sau:
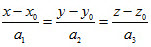
Ví dụ 1. Viết phương trình tham số của đường thẳng 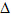 đi qua điểm M0 (1;2;3) và có vecto chỉ phương là đi qua điểm M0 (1;2;3) và có vecto chỉ phương là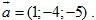
Giải
Phương trình tham số của 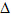 là : là : 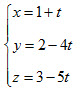
Ví dụ 2. Viết phương trình tham số của đường thẳng AB với A(1 ; -2 ; 3) và B(3 ; 0 ; 0).
Giải

Giải

Hãy tìm toạ độ của một điểm M trên 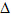 và toạ độ một vecto chỉ phương của và toạ độ một vecto chỉ phương của 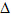 . .
II – ĐIỀU KIỆN ĐỂ HAI ĐƯỜNG THẲNG SONG SONG, CẮT NHAU, CHÉO NHAU
3 Cho hai đường thẳng d và d’ có phương trình tham số lần lượt là
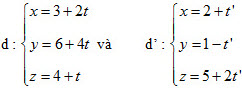
a) Hãy chứng tỏ điểm M(1 ; 2 ; 3) là điểm chung của d và d’ ;
b) Hãy chứng tỏ d và d’ có hai vecto chỉ phương không cùng phương.
Trong không gian Oxyz cho hai đường thẳng d, d’ có phương trình tham số lần lượt là
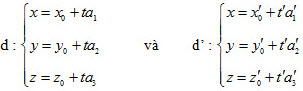
Sau đây ta xét vị trí tương đối giữa d và d’, nghĩa là xét điều kiện để d và d’ song song, cắt nhau hoặc chéo nhau.
1. Điều kiện để hai đường thẳng song song
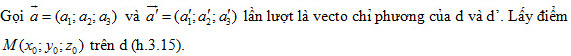
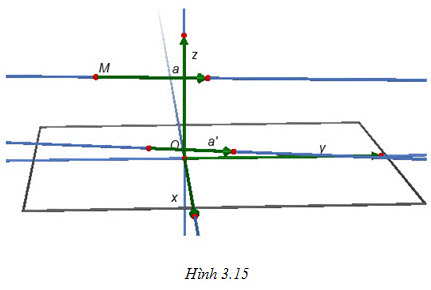
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch3_h3.15.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Ta có :

Giải

2. Điều kiện để hai đường thẳng cắt nhau
Hai đường thẳng d và d’ cắt nhau khi và chỉ khi hệ phương trình ẩn t, t’ sau
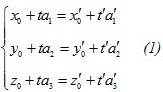
có đúng một nghiệm.
Chú ý. Giả sử hệ (1) có nghiệm t0t0, để tìm giao điểm M0¬ của d và d’ ta có thể thay t0 vào phương trình tham số của d hoặc thay t0 vào phương trình tham số của d’.
Ví dụ 2. Tìm giao điểm của hai đường thẳng sau:
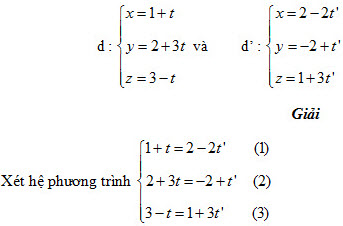
Từ (1) và (2) suy ra t = -1 và t’ = 1. Thay vào phương trình (3) ta thấy nó thoả mãn. Vậy hệ phương trình trên có nghiệm là t = -1, t’ = 1.
Suy ra d cắt d’ tại điểm M(0 ; -1 ; 4).
3. Điều kiện để hai đường thẳng chéo nhau
Ta biết rằng hai đường thẳng chéo nhau nếu chúng không cùng phương và không cắt nhau. Do vậy
Hai đường thẳng d và d’ chéo nhau khi và chỉ khi 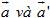 không cùng phương và hệ phương trình không cùng phương và hệ phương trình
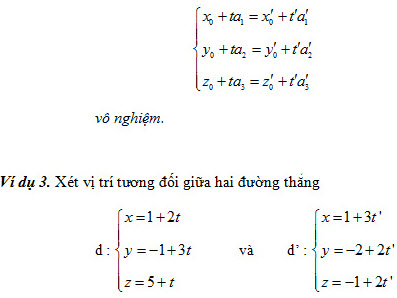
Giải
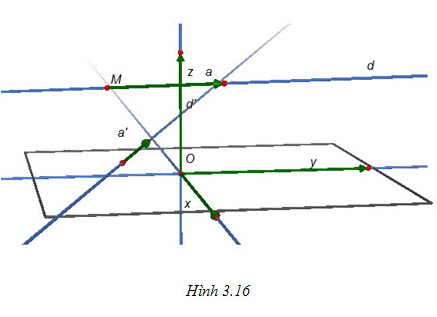
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch3_h3.16.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )

Giải

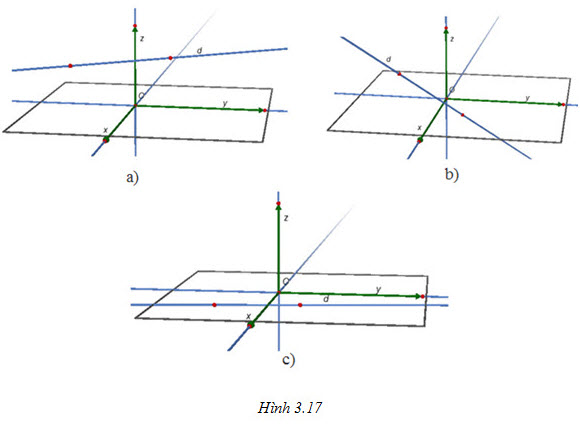
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch3_h3.17a.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch3_h3.17b.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12cb_Ch3_h3.17c.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
- Nếu phương trình (1) có đúng một nghiệm t = t0 thì d cắt 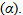 tại điểmM0 (x0+t0a1; y0+t0a2;
z0+t0a3) (h.3.17b) tại điểmM0 (x0+t0a1; y0+t0a2;
z0+t0a3) (h.3.17b)
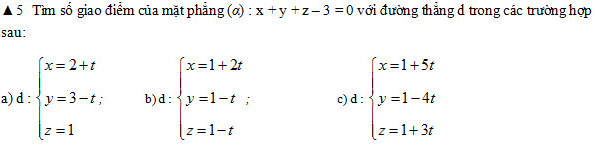
BÀI TẬP
1. Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau:

lần lượt trên các mặt phẳng sau:
a) (Oxy);
b) (Oyz).
3. Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau:
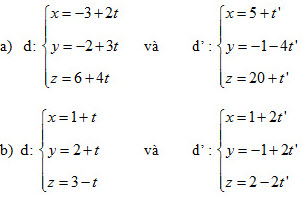
4. Tìm a để hai đường thẳng sau đây cắt nhau
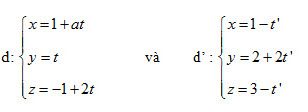
5. Tìm số giao điểm của đường thẳng d với mặt phẳng 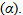 trong các trường hợp sau: trong các trường hợp sau:
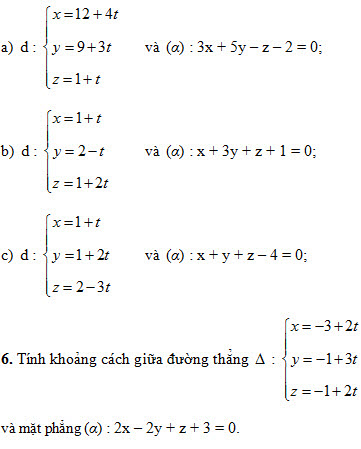
a) Tìm toạ độ điểm H là hình chiếu vuông góc của điểm A trên đường thẳng 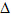 . .
b) Tìm toạ độ điểm A’ đối xứng với A qua đường thẳng 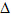 . .
8. Cho điểm M(1 ; 4 ; 2) và mặt phẳng 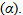 : x + y + z - 1 = 0. : x + y + z - 1 = 0.
a) Tìm toạ độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng 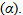
b) Tìm toạ độ điểm M’ đối xứng với M qua mặt phẳng (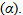
c) Tính khoảng cách từ điểm M đến mặt phẳng 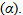
9. Cho hai đường thẳng
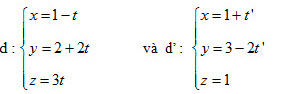
Chứng minh d và d’ chéo nhau.
10. Giải bài toán sau đây bằng phương pháp toạ độ:
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Tính khoảng cách từ đỉnh A đến các mặt phẳng (A’BD) và (B’D’C).
Schoolnet
|

 Xem giỏ hàng
Xem giỏ hàng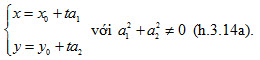



 đi qua điểmM0 (x0; y0 ; z0 ) và nhận
đi qua điểmM0 (x0; y0 ; z0 ) và nhận 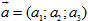 làm vecto chỉ phương.
làm vecto chỉ phương. 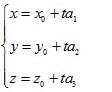

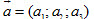
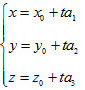
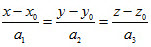
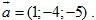
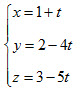


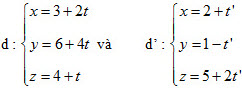
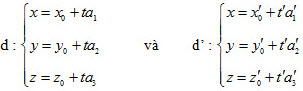
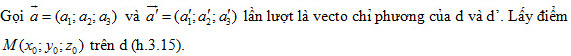



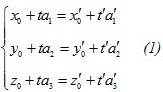
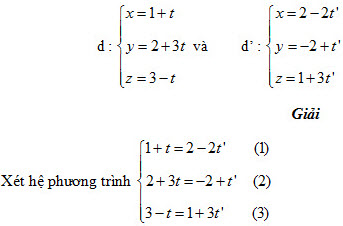
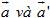 không cùng phương và hệ phương trình
không cùng phương và hệ phương trình 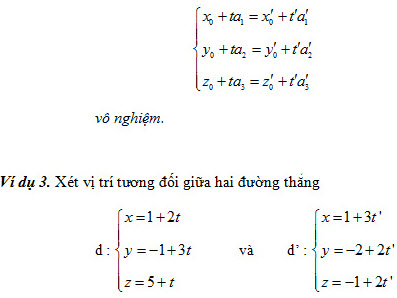




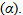 tại điểmM0 (x0+t0a1; y0+t0a2;
z0+t0a3) (h.3.17b)
tại điểmM0 (x0+t0a1; y0+t0a2;
z0+t0a3) (h.3.17b)